Solving two-parameter eigenvalue problems using an alternating method
Notebook.Contents:
We want to find solutions of the two-parameter eigenvalue problem
The eigenvalues are the intersection points of the two eigencurves associated to each equation, here depicted in blue and orange:
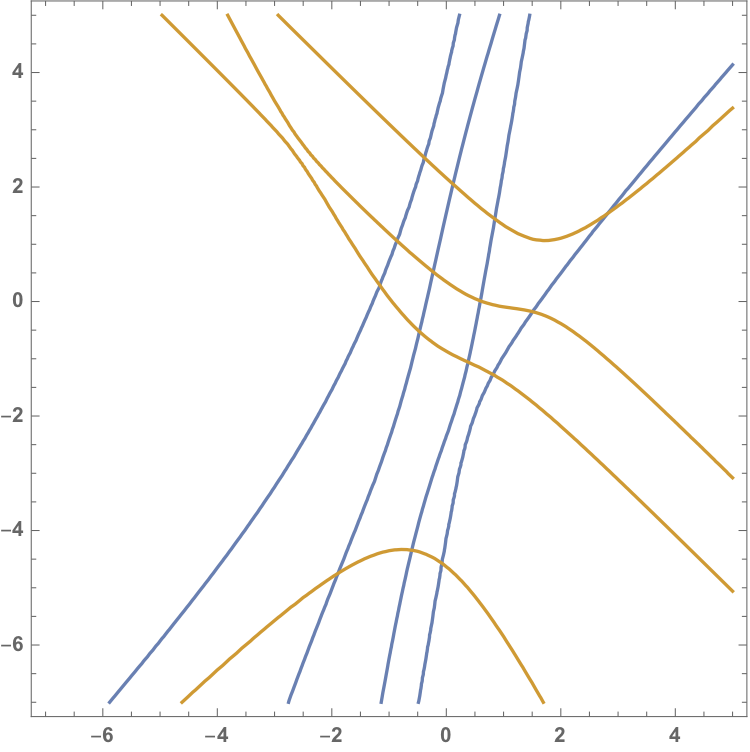
If the matrix \(C_1\otimes B_2-B_1\otimes C_2\) is definite, every yellow curve intersects every blue curve exactly once. The alternating algorithm can then be interpreted in the following way:
And repeating. This is illustrated in the following picture:
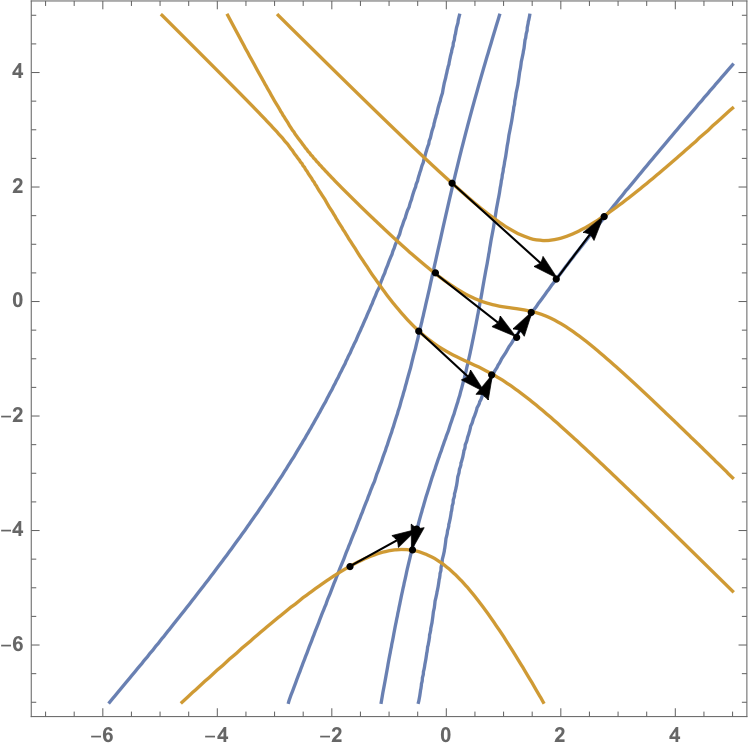
The arrows show the iterates. This interpretation allows us to provide a local quadratic convergence of our algorithm
The code is presented as a Jupyter notebook in Julia which can be downloaded here: TwoParameterNotebook.ipynb.
Project page created: 26/05/2021
Project contributors: Henrik Eisenmann, Yuji Nakatsukasa
Jupyter notebook written by: Henrik Eisenmann, 26/05/21
Software used: Julia (Version 1.5.2)
Corresponding author of this page: Henrik Eisenmann, henrik.eisenmann@mis.mpg.de