Problem 11

Draw a quintic curve in \(\mathbb{R}^2\) with 7 connected components, and draw a quartic surface in \(\mathbb{R}^3\) with 11 connected components.

Solution

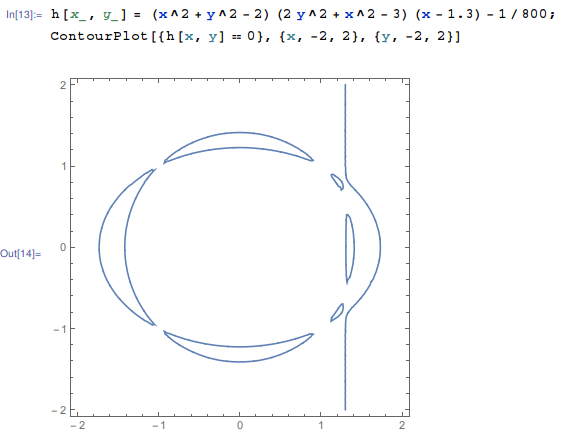
A quintic curve in \(\mathbb{R}^2\) with 7 connected components in Mathematica:

h[x_, y_] = (x^2 + y^2 - 2) (2 y^2 + x^2 - 3) (x - 1.3) - 1/800;
ContourPlot[{h[x, y] == 0}, {x, -2, 2}, {y, -2, 2}]
../_images/11_a.png

A quartic surface in \(\mathbb{R}^3\) with 11 connected components in Surfer:

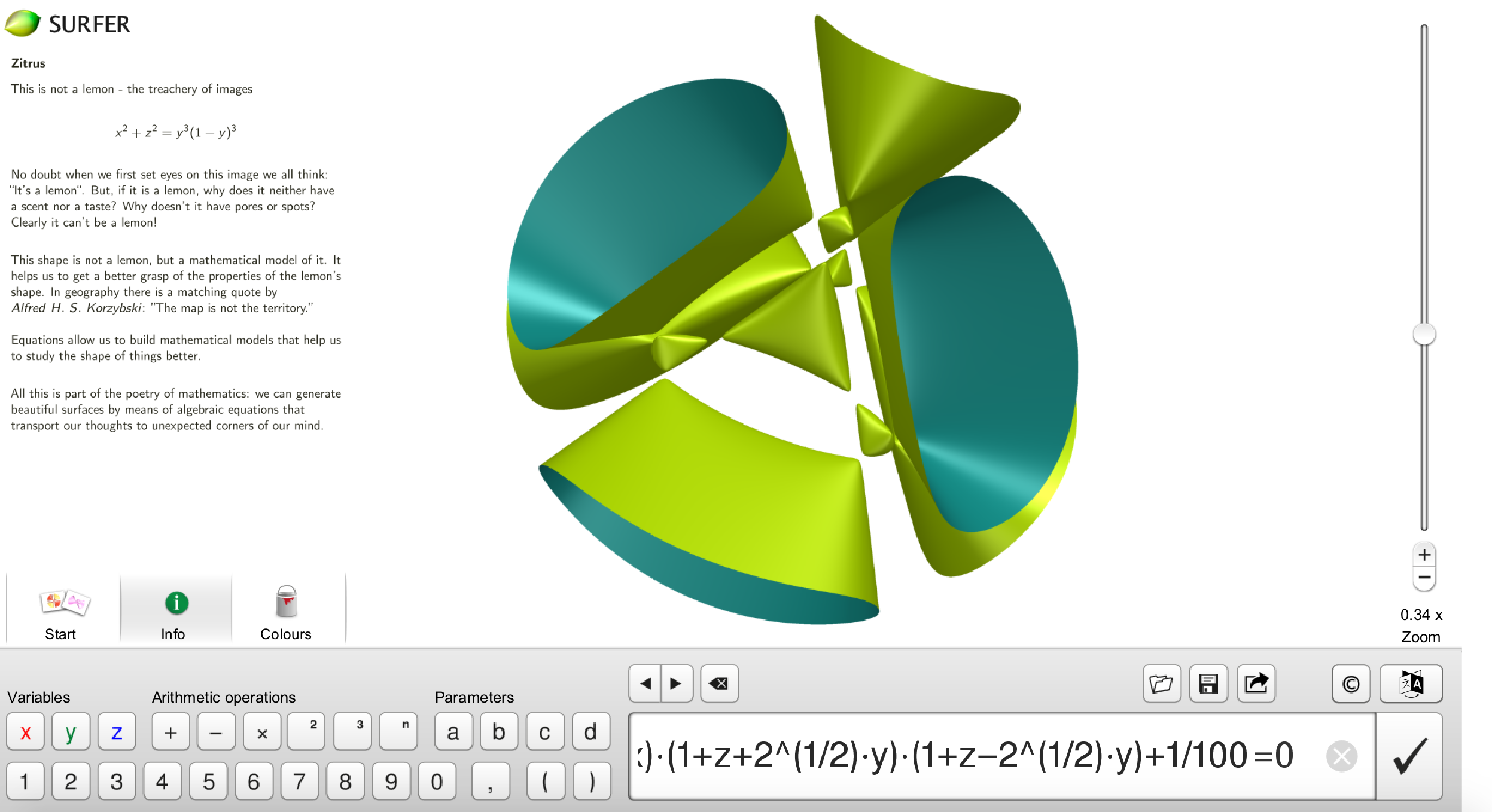
../_images/11_b.png

The equation is given by:

(x^2+y^2+z^2-2)^2-5*(1-z-2^(1/2)*x)*(1-z+2^(1/2)*x)*(1+z+2^(1/2)*y)*(1+z-2^(1/2)*y)=0