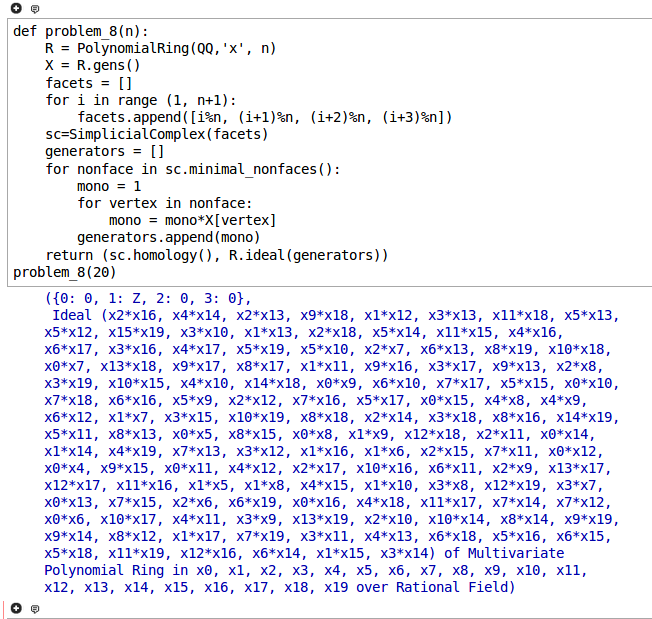
Problem 8

Consider the three-dimensional simplicial complex on \(n\) vertices having the \(n\) facets \(\{i,i+1,i+2,i+3\}\), for \(i=1,2,\ldots,n\), cyclically rotated. For \(n \leq 20\), compute the Stanley-Reisner ideals and all homology groups.

Solution

Here is a solution in Sage:

def problem_8(n):
    R = PolynomialRing(QQ,'x', n)
    X = R.gens()
    facets = []
    for i in range (1, n+1):
        facets.append([i%n, (i+1)%n, (i+2)%n, (i+3)%n])
    sc=SimplicialComplex(facets)
    generators = []
    for nonface in sc.minimal_nonfaces():
        mono = 1
        for vertex in nonface:
            mono = mono*X[vertex]
        generators.append(mono)
    return (sc.homology(), R.ideal(generators))

problem_8(20)