Problem 13

Draw a unimodular triangulation of 4 times the unit tetrahedron. Draw the smooth tropical quartic surface that is dual to your triangulation.

Solution

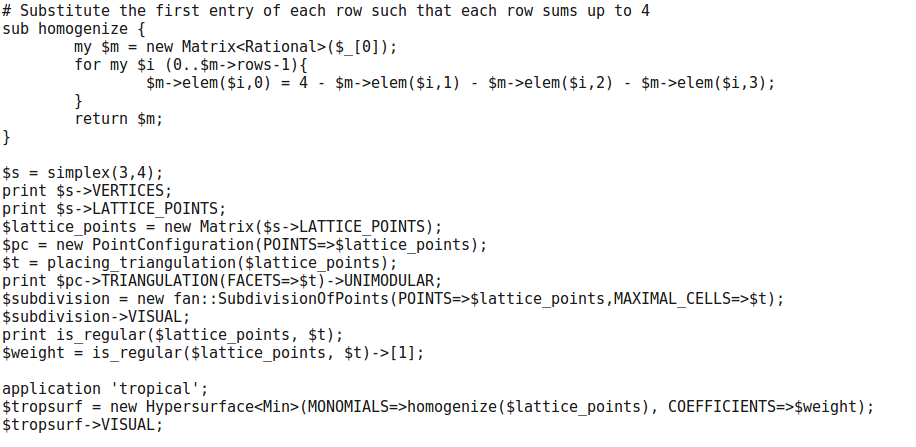
In Polymake:

Substitute the first entry of each row such that each row sums up to 4

sub homogenize {
    my $m = new Matrix<Rational>($_[0]);
    for my $i (0..$m->rows-1){
        $m->elem($i,0) = 4 - $m->elem($i,1) - $m->elem($i,2) - $m->elem($i,3);
    }
    return $m;
}

$s = simplex(3,4);
print $s->VERTICES;
print $s->LATTICE_POINTS;
$lattice_points = new Matrix($s->LATTICE_POINTS);
$pc = new PointConfiguration(POINTS=>$lattice_points);
$t = placing_triangulation($lattice_points);
print $pc->TRIANGULATION(FACETS=>$t)->UNIMODULAR;
$subdivision = new fan::SubdivisionOfPoints(POINTS=>$lattice_points,MAXIMAL_CELLS=>$t);
$subdivision->VISUAL;
print is_regular($lattice_points, $t);
$weight = is_regular($lattice_points, $t)->[1];

application 'tropical';
$tropsurf = new Hypersurface<Min>(MONOMIALS=>homogenize($lattice_points), COEFFICIENTS=>$weight);
$tropsurf->VISUAL;