Adjoints and Canonical Forms of Polypols
ABSTRACT: Polypols are natural generalizations of polytopes, with boundaries given by nonlinear algebraic hypersurfaces. We describe polypols in the plane and in 3-space that admit a unique adjoint hypersurface and study them from an algebro-geometric perspective. We relate planar polypols to positive geometries introduced originally in particle physics, and identify the adjoint curve of a planar polypol with the numerator of the canonical differential form associated with the positive geometry. We settle several cases of a conjecture by Wachspress claiming that the adjoint curve of a regular planar polypol does not intersect its interior. In particular, we provide a complete characterization of the real topology of the adjoint curve for arbitrary convex polygons. Finally, we determine all types of planar polypols such that the rational map sending a polypol to its adjoint is finite, and explore connections of our topic with algebraic statistics.
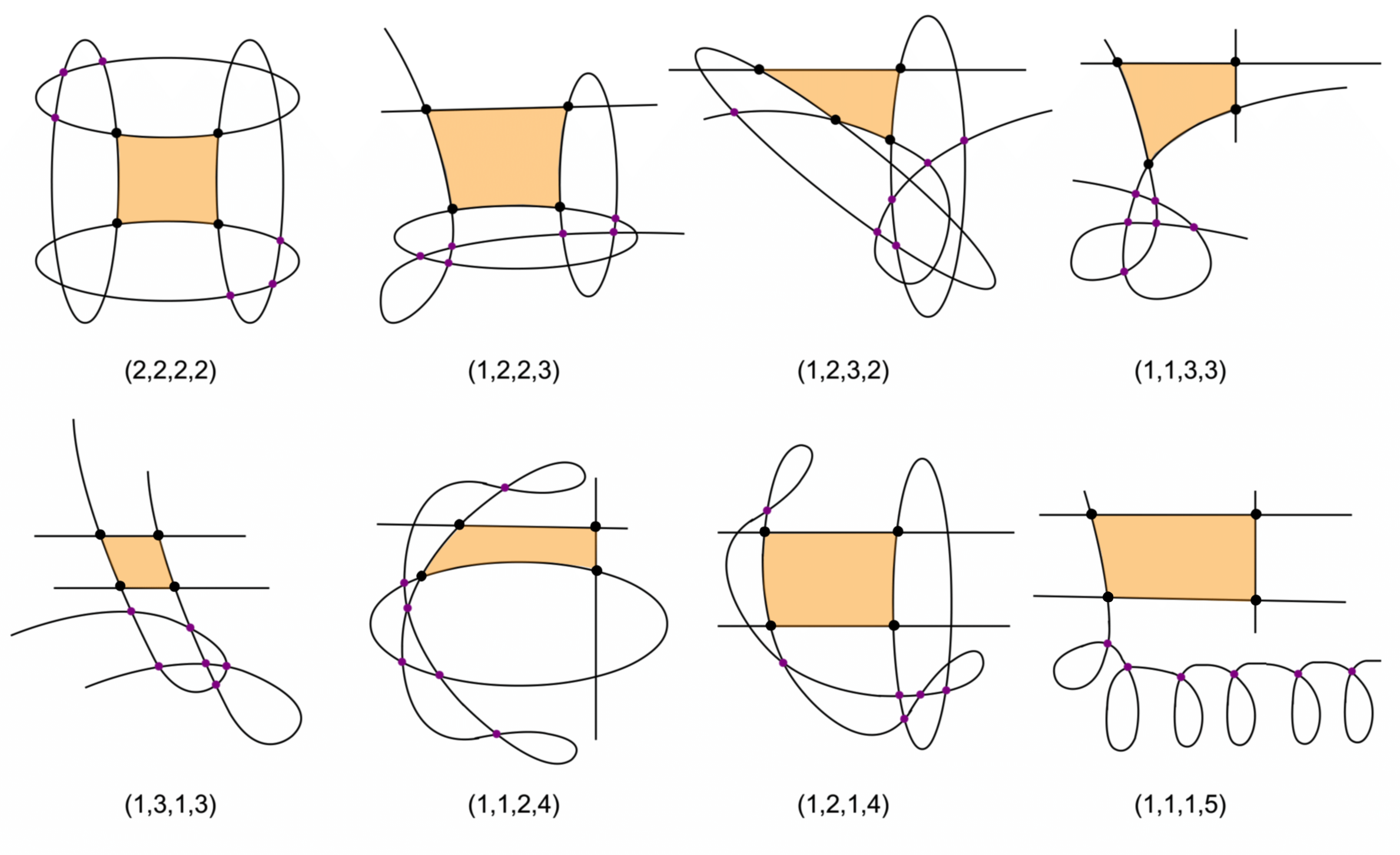
The code included here illustrates some results from Section 4 in the paper, in which we investigate types of polypols with a finite adjoint map. Of all types illustrated in the figure below, we show that (1,3,1,3) is the only one that does not have this property, and the other 7 types are the only ones that do (Theorem 4.2 and Proposition 4.5).
All of our code is written in julia using the packages HomotopyContinuation.jl (v2.5.6) and EigenvalueSolver.jl.
The certificates used in Theorem 4.2 and Proposition 4.5 can be downloaded here certificates.zip. These can be reproduced using the code in code.zip.
Project page created: 25/08/2021
Project contributors: Kathlén Kohn, Ragni Piene, Kristian Ranestad, Felix Rydell, Boris Shapiro, Rainer Sinn, Miruna-Stefana Sorea, Simon Telen
Corresponding author of this page: Simon Telen, Simon.Telen@mis.mpg.de
Software used: Julia (Version 1.5.2)