Bayesian Integrals on Toric Varieties
ABSTRACT: We explore the positive geometry of statistical models in the setting of toric varieties. Our focus lies on models for discrete data that are parameterized in terms of Cox coordinates. We develop a geometric theory for computations in Bayesian statistics, such as evaluating marginal likelihood integrals and sampling from posterior distributions. These are based on a tropical sampling method for evaluating Feynman integrals in physics. We here extend that method from projective spaces to arbitrary toric varieties.
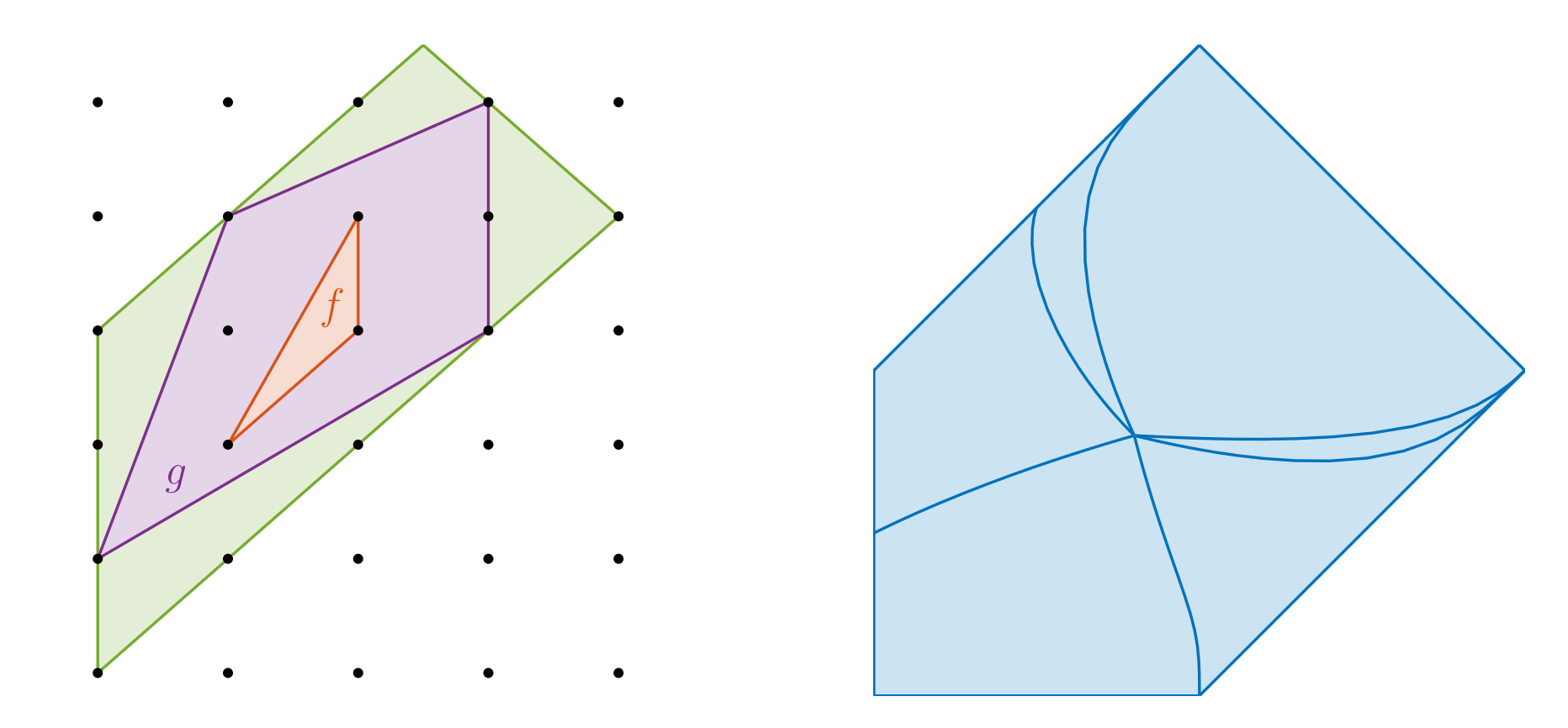
As an illustration, the following figure shows the sector decomposition of a pentagon as seen in Example 4.5.
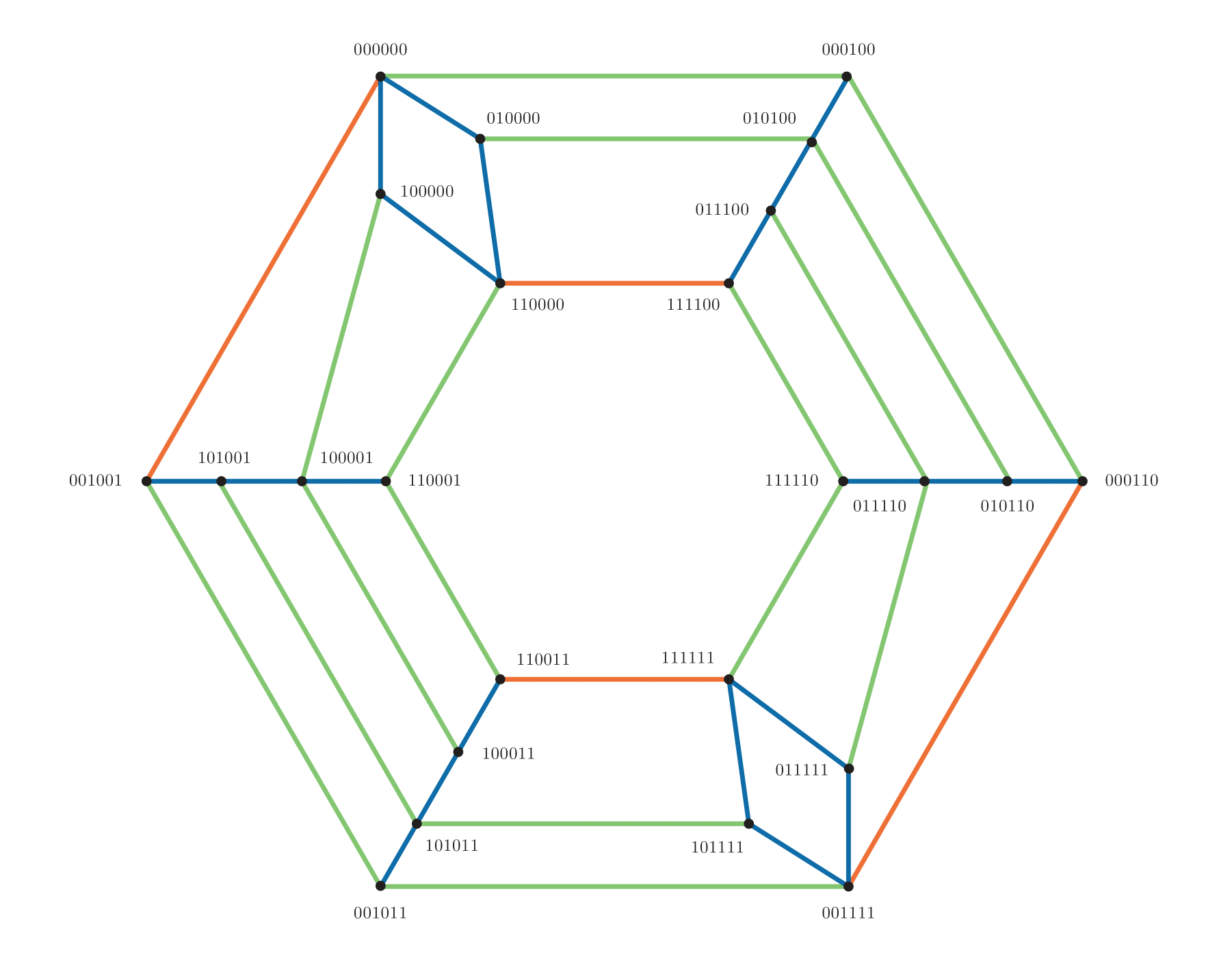
The paper also features a polytope arising from a three-dimensional conditional independence model. Its Schlegel diagram is shown below.
Our algorithms are implemented julia. The code can be downloaded here julia_code.zip. It is illustrated in the following notebook:
Project page created: 15/04/2022
Project contributors: Michael Borinsky, Anna-Laura Sattelberger, Bernd Sturmfels, Simon Telen
Corresponding author of this page: Simon Telen, Simon.Telen@mis.mpg.de
Software used: Julia (Version 1.7.1)