
Hilbert Functions of Chopped Ideals
Overview
Abstract. A chopped ideal is obtained from a homogeneous ideal by considering only the generators of a fixed degree. We investigate cases in which the chopped ideal defines the same finite set of points as the original one-dimensional ideal. The complexity of computing these points from the chopped ideal is governed by the Hilbert function and regularity. We conjecture values for these invariants and prove them in many cases. We show that our conjecture is of practical relevance for symmetric tensor decomposition.
On this page you can find the code and data used to prove Theorem 5.1 and the implementation of numerical symmetric tensor decomposition using eigenvalue methods in Julia. We also indicate how to verify and reproduce our computational claims. Additionally we show some visualizations for the case example of 18 points in the plane and of the saturation gaps.
Macaulay2 source code
ChoppedIdeals.m2Certificates for Thm. 5.1 available on KEEPER
Julia source code
Catalecticant.zip
18 points in the plane
We recall the setting of the paper. Let \(Z=\{z_1,\dots,z_r\}\subseteq \mathbb{P}^n\) be a general set of points, and \(d\geq 0\). We are interested in comparing the ideals \(I := I(Z)\) and \(I_{\langle d \rangle} := \langle I_d\rangle_S\), in particular, when the graded components coincide. This problem occurs somewhat naturally in the setting of “low rank” symmetric tensor decomposition, when only equations of a certain degree are readily availably.
The smallest interesting example occurs for \(r=18\) general points \(Z\) in the plane. In the tensor setting, this corresponds to a general rank \(18\) form of degree \(10\) in \(3\) variables.
loadPackage "Points"
I = randomPoints(2,18);
Ichop = ideal super basis(5,I);
I == Ichop
for t to 10 list {t, hilbertFunction(t,I), hilbertFunction(t,Ichop)}
The lowest nonzero component \(I_5\) is generated by \(\binom{5+2}{2} - 18 = 3\) quintics \(q_1,q_2,q_3\), here is a randomly generated example:

These polynomials do not generate \(I\), indeed, there is a minimal generator in \(I_6\) is missing. The Hilbert functions of the two ideals are as follows:
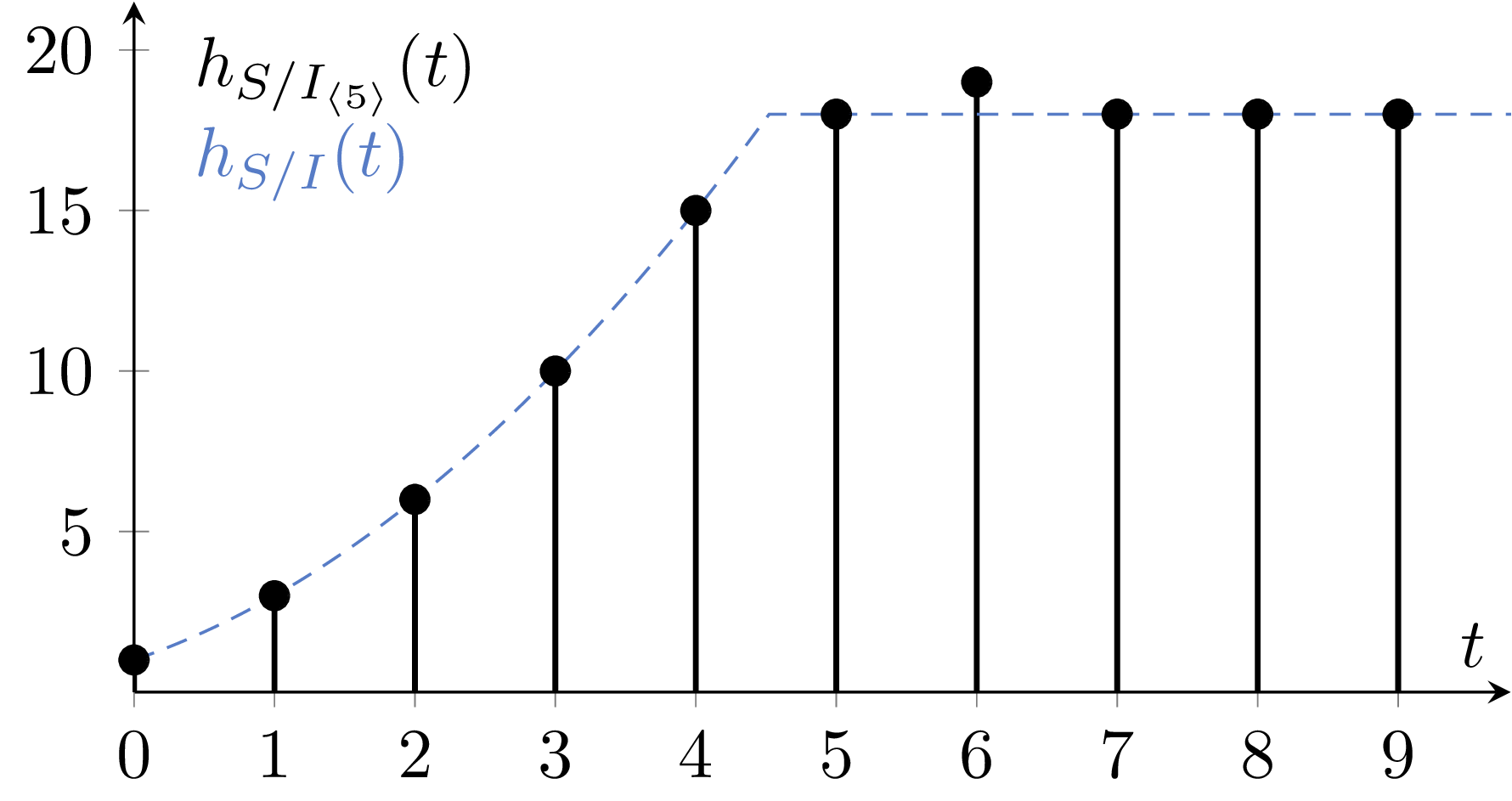
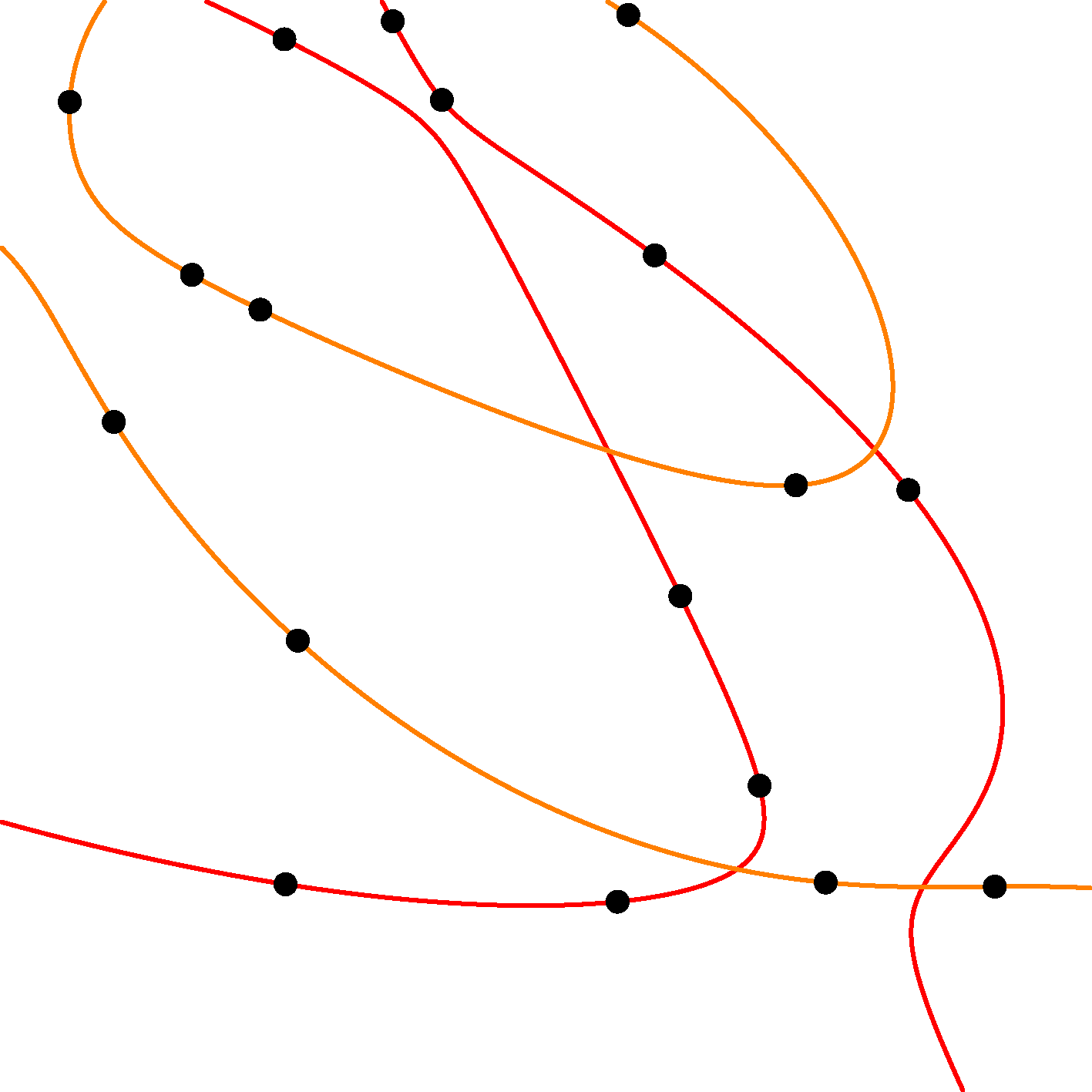
Which generator of \(I_6\) is missing? Splitting the points in groups of \(9+9\), there is a unique cubic through each group. Their product spans a complement of \((I_{\langle 5 \rangle})_6\) in \(I_6\) (Proposition 3.1). Here is one such partition in the previous example:
Verifying the conjecture - Thm. 5.1
To verify cases of the Expected Syzygy Conjecture you need Macaulay2 and the file ChoppedIdeals.m2.
To test a specific case \((n,r)\) you can simply type
load "ChoppedIdeals.m2";
(n,r) = (2,31);
(Z,I) = testCase(n,r);
To verify our certificates download them from KEEPER (you can also select a subset or only specific files).
Place the text files in a directory together with ChoppedIdeals.m2.
load "ChoppedIdeals.m2";
verifyDirectory "."
You may want to organize them in a different directory, then you have to replace "." in the previous line.
You can also certify individual certificates, e.g. “d07_r0032.txt” using
verifyCertificate "d07_r0031.txt"
For details about the computation check the commented Macaulay2 code.
Numerical experiments with Julia
To test the numerical symmetric tensor application of chopped ideals download the Julia code Catalecticant.zip.
Extract the files and follow the instructions in “examples.jl”, after loading the packages you can execute the example file line by line and follow along.
Visualizing the saturation gaps
The following diagrams show the saturation gaps for various numbers of general points. The case of 18 points in the plane is the gap \([5,7]\). Generally, a gap \([d,d+e_0]\) indicates that \(d\) is the lowest degree in which \(I(Z)\) has equations (also its Hilbert regularity) and \(e_0>0\) is minimal such that \((I_{\langle d \rangle})_{d+e_0} = I_{d+e_0}\). This is the interval in which the Hilbert function \(h_{S/I_{\langle d \rangle}}(t)\) will exceed \(h_{S/I}(t)\) in the case \(e_0>1\).
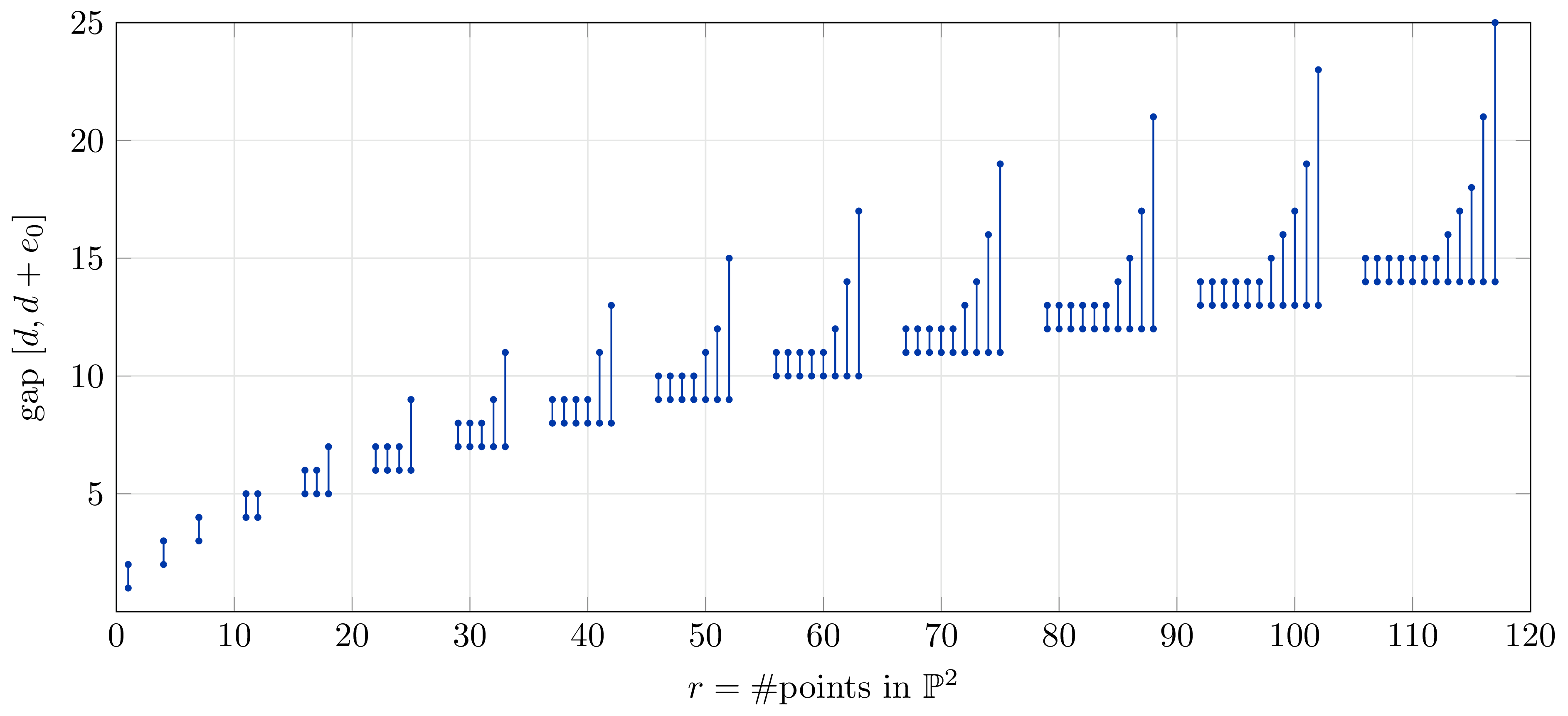
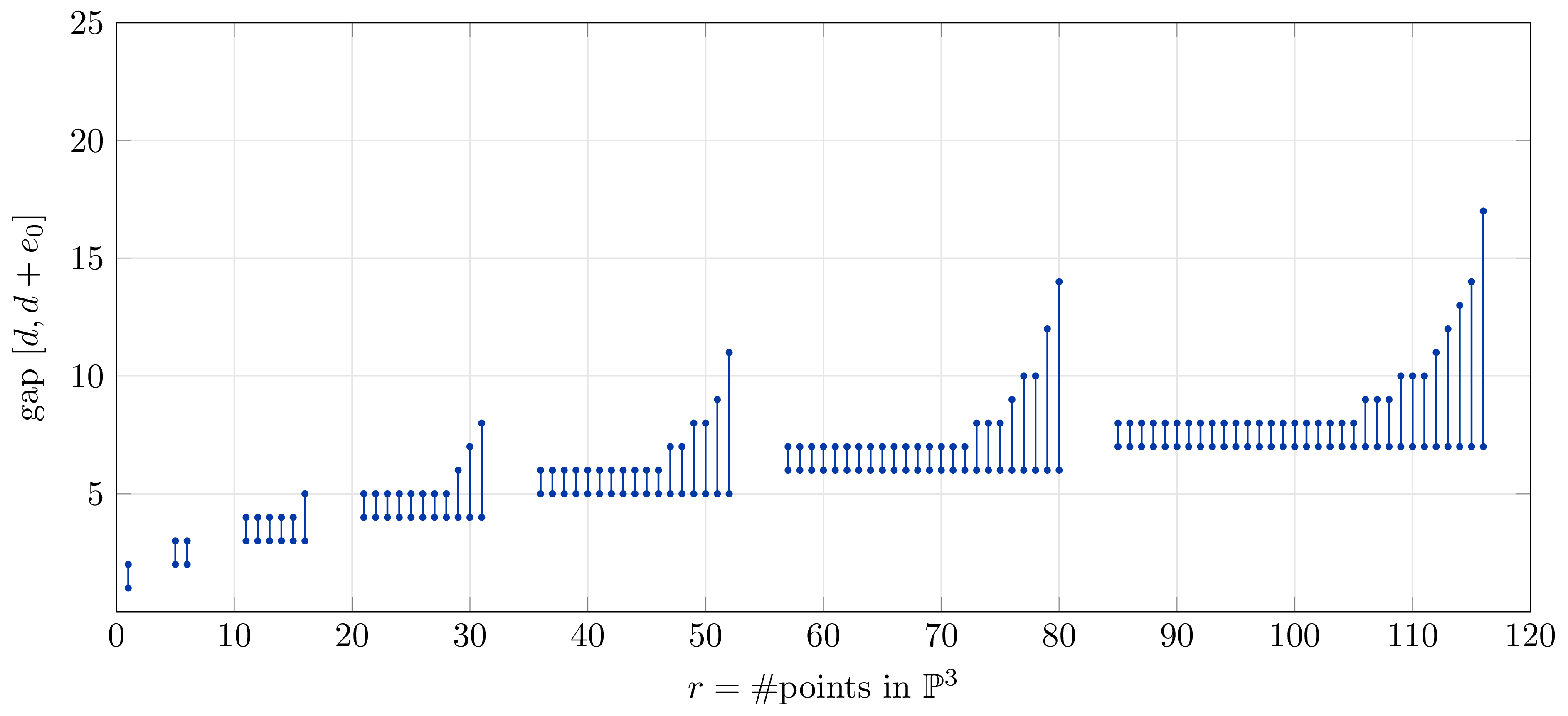
Project page created: 10/07/2023
Project contributors: Fulvio Gesmundo, Leonie Kayser, Simon Telen
Corresponding author of this page: Leonie Kayser, kayser@mis.mpg.de
Macaulay2 code written by: Leonie Kayser
Julia code written by: Simon Telen
Software used: Macaulay2 (v1.21), Julia (v1.8.3)
System setup used:
Macaulay2 (v1.21): MPI MiS Compute Server (4x 18-Core Intel Xeon E7-8867 v4 at 2.4 GHz, 3072 GB RAM)
Julia (v1.8.3): MacBook Pro with Intel Core i7 processor at 2.6 GHz, 16 GB RAM
License for code of this project page: MIT License (https://spdx.org/licenses/MIT.html)
License for all other content of this project page (text, images, …): CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/)
Last updated 12/10/2023.