Computational Complexity of Polynomial Subalgebras
Overview
Abstract. The computational complexity of polynomial ideals and Gröbner bases has been studied since the 1980s. In recent years the related notions of polynomial subalgebras and SAGBI bases have gained more and more attention in computational algebra, with a view towards effective algorithms. We investigate the computational complexity of the subalgebra membership problem and degree bounds. In particular, we place these problems in the complexity class EXPSPACE and prove PSPACE-completeness for homogeneous algebras. We highlight parallels and differences compared to the settings of ideals and also look at important classes of polynomials such as monomial algebras.
On this page you can find the Macaulay2 code and elaboration for the binary counting homogeneous polynomial algebra from Theorem 4.3.
The LBA
A linearly bounded automaton counting all binary numbers from 000 to 111 can be implemented as sketched in Example 2.2.
↓ |
||||
▷ |
0 |
0 |
0 |
◁ |
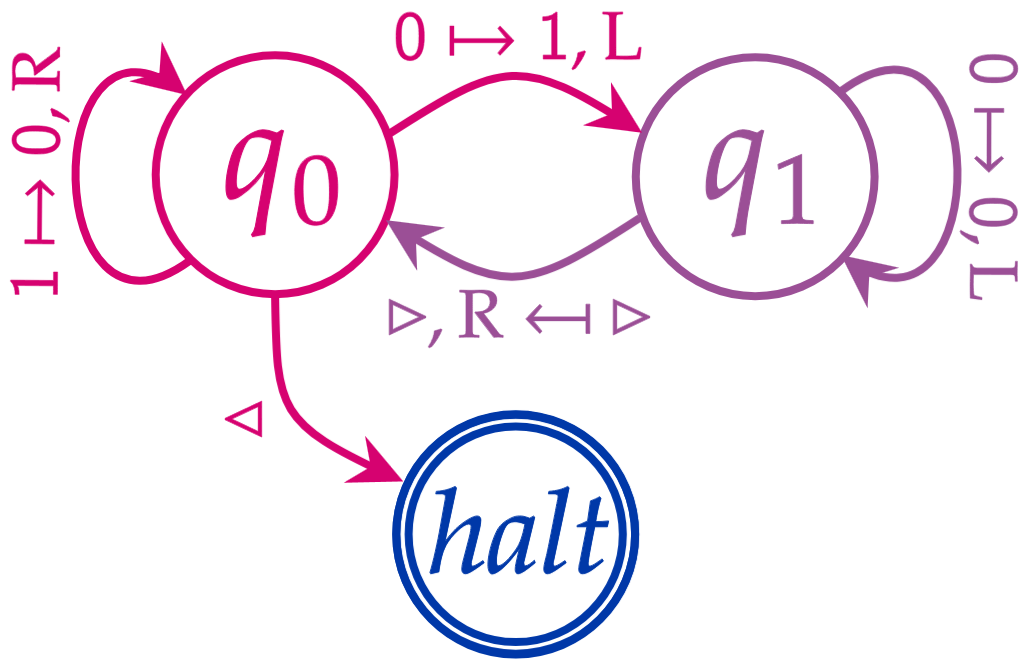
There are two states \(q_0,q_1\) plus the halting state.
\(q_0\): If the current symbol is 1, then write 0, move right and repeat until we reach a 0 or ◁. In the first case write 1, step left and go to \(q_0\). In the second case halt.
\(q_1\): If the current symbol is not ▷, then write 0 and step left. If it is ▷, then step right and go to \(q_0\).
The way our tape is structured, we only need to specify five of the \(2\cdot 4 = 8\) possible transitions:
▷ |
0 |
1 |
◁ |
|
|---|---|---|---|---|
\(q_0\) |
(\(q_1\),1,L) |
(\(q_0\),0,R) |
halt |
|
\(q_1\) |
(\(q_0\),▷,R) |
(\(q_1\),0,L) |
This can also be represented in the state diagram
You can see the sequence of configurations on the start configuration 000 on this subpage.
The subalgebra
The translation into a subalgebra is made by encoding a configuration by a monomial of degree \(n+2\), where \(n\) is the number of digits (in the example on this page n=3). The monomial for a configuration in state \(q_i\) with head at position \(0\leq j \leq n\) with tape \(\triangleright b_1\dots b_{n}\triangleleft\) is
This deviates slightly from the notation in the proof of Theorem 4.3 to make the code more readable. The four non-halting transitions become
\((q_0,0)\mapsto (q_1,1,\mathrm{L})\) |
becomes |
\(Q_0H_iO_i - Q_1H_{i-1}I_i\), |
\(1\leq i \leq n\) |
\((q_0,1)\mapsto (q_0,0,\mathrm{R})\) |
becomes |
\(Q_0H_iI_i - Q_0H_{i+1}O_i\), |
\(1\leq i \leq n-1\) |
\((q_1,0)\mapsto (q_1,0,\mathrm{L})\) |
becomes |
\(Q_1H_iO_i - Q_1H_{i-1}O_i\), |
\(1\leq i \leq n\) |
\((q_1,\triangleright)\mapsto (q_0,\triangleright,\mathrm{R})\) |
becomes |
\(Q_1H_0 - Q_0H_1\) |
The start configuration from above is \(Q_0H_1O_1\dotsm O_n\). The last configuration representable without ◁ (before the “halt state”) is
↓ |
||||
▷ |
0 |
0 |
1 |
◁ |
which corresponds to \(Q_0H_nO_1\dotsm O_{n-1}I_n\).
In our example (n=3) it takes 24 transitions between these configurations, so any subalgebra membership certificate has at least 24 terms. This is already to big to terminate using the built-in functionality naively on my computer. The case n=2 runs in less than a second and correctly produces the 9 transitions required.
The Macaulay2 code can be downloaded here:
BinCountAlgebra.m2
Project page created: 30/01/2025
Project contributors: Leonie Kayser
Corresponding author of this page: Leonie Kayser, kayser@mis.mpg.de
Software used: Macaulay2 (v1.22)
System setup used:
Macaulay2 (v1.22): MacBook Pro with Intel Core i7 processor at 2.6 GHz, 16 GB RAM
License for code of this project page: MIT License (https://spdx.org/licenses/MIT.html)
License for all other content of this project page (text, images, …): CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/)
Last updated 08/04/2025.