Enumerating Chambers of Hyperplane Arrangements with Symmetry

This page contains auxiliary material to the paper:

Taylor Brysiewicz, Holger Eble, and Lukas Kühne: Computing characteristic polynomials of hyperplane arrangements with symmetries

In: Discrete and computational geometry, 70 (2023) 4, p. 1356-1377

DOI: 10.1007/s00454-023-00557-2 ARXIV: https://arxiv.org/abs/2105.14542 CODE: https://mathrepo.mis.mpg.de/CountingChambers

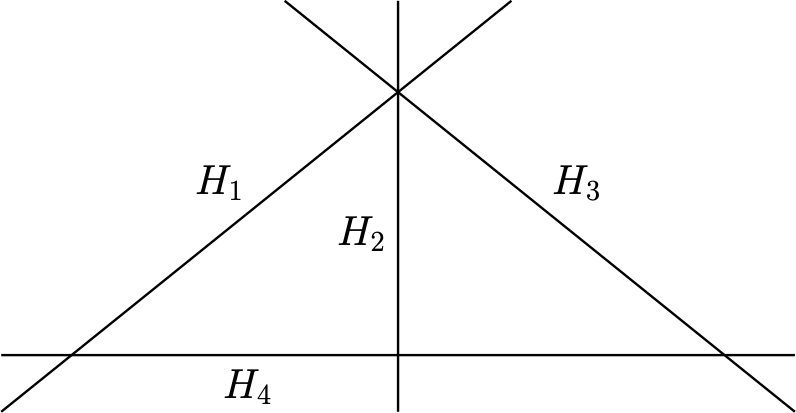
The above picture shows an example of a hyperplane arrangement in the plane consisting of four hyperplanes. The complement consists of ten chambers.

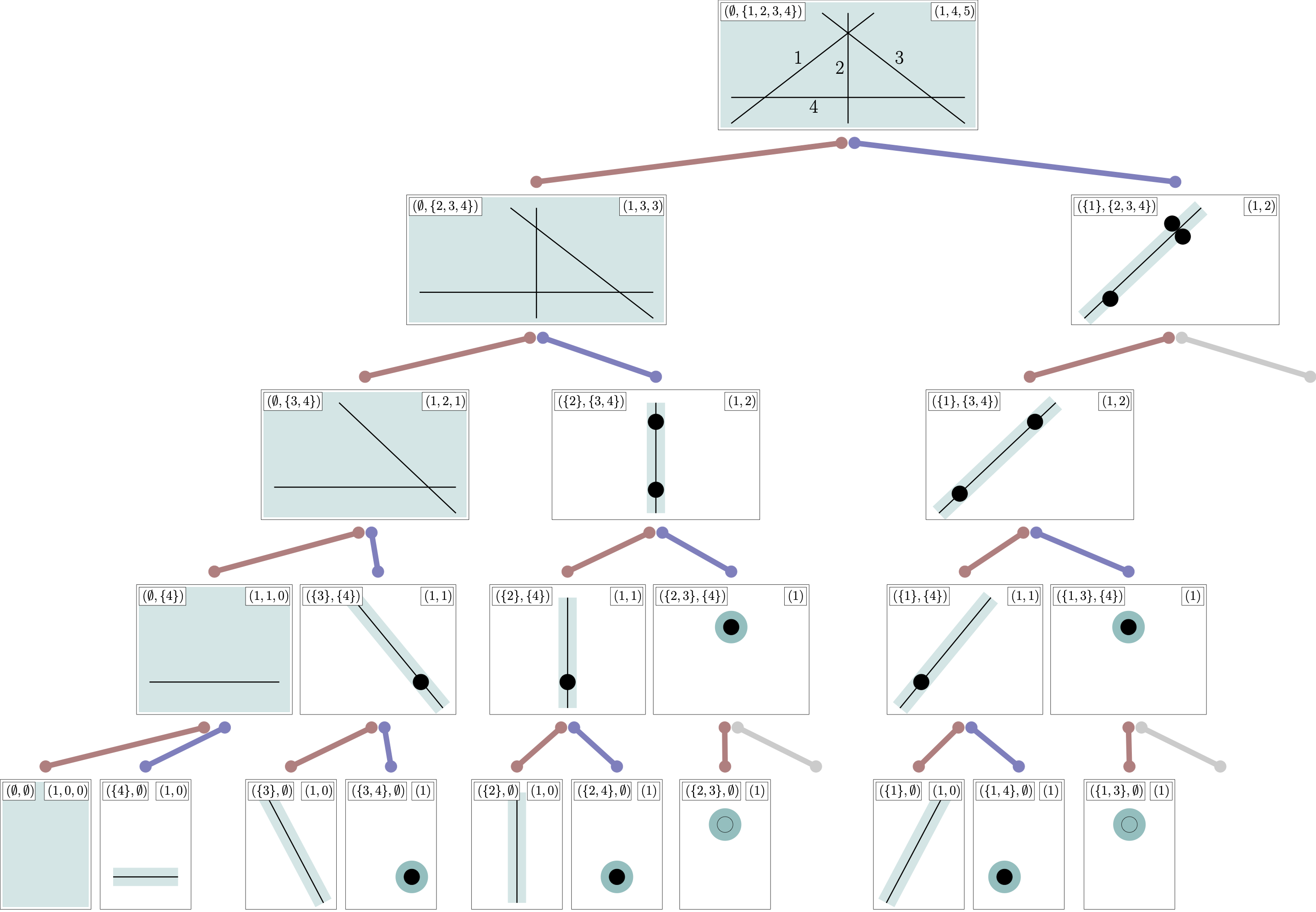
One way of counting these chambers is through a deletion-restriction tree depicted below.

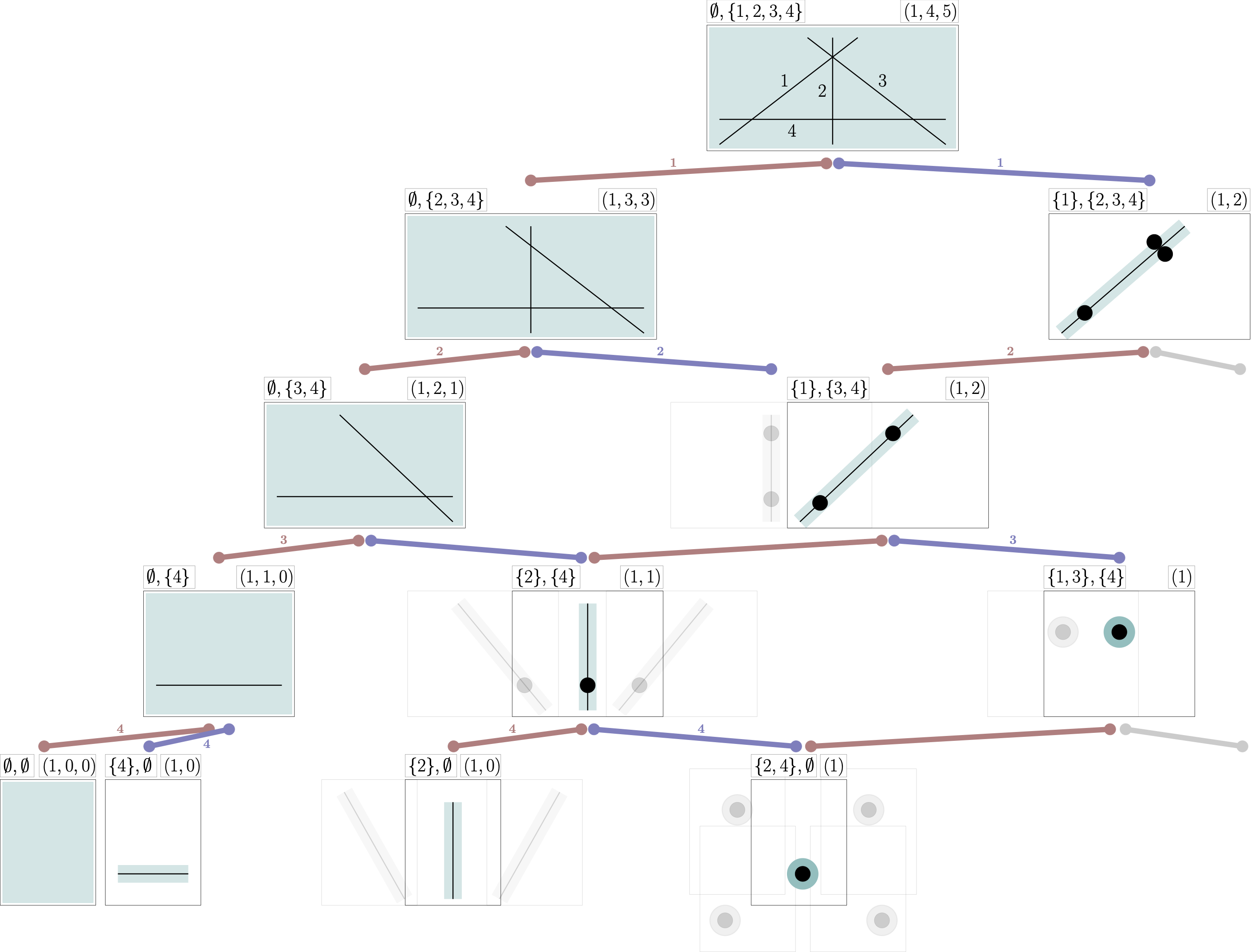
Our paper outlines a novel algorithm to count chambers of hyperplane arrangments taking advantage their symmetry. This yields the following reduced algorithmic structure.

Our chamber counting algorithm is implemented in julia using OSCAR.jl. It can perform this task for arrangements with over a quadrillion chambers. Our implementation is publicly available here: CountingChambers.jl.

The following Jupyter notebooks illustrate how to use our software.

• Enumerating chambers in symmetric arrangements

You may also run this file online yourself by clicking the link below.

Project page created: 25/05/2021

Project contributors: Taylor Brysiewicz, Holger Eble, and Lukas Kühne

Corresponding author of this page: Lukas Kühne, lukas.kuhne@mis.mpg.de

Software used: Julia (Version 1.6.0), GAP