Experiment 3: Solving equations on a weighted projective space
We generate a system of polynomial equations that have solutions of large modulus. Many solvers prematurely truncate these paths and do not compute these solutions. These equations homogenize to equations on a weighted projective space, where we compute all solutions.
We activate the project’s environment.
[1]:
using Pkg
Pkg.activate(".")
Activating environment at `~/Documents/Projects/cox-homotopies/code_cox_homotopies_fix/Project.toml`
We include our methods below.
[2]:
include("CoxHomotopy.jl")
polymake version 4.2
Copyright (c) 1997-2020
Ewgenij Gawrilow, Michael Joswig, and the polymake team
Technische Universität Berlin, Germany
https://polymake.org
This is free software licensed under GPL; see the source for copying conditions.
There is NO warranty; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
[2]:
trackPathRandom (generic function with 1 method)
The following code generates a system that homogenizes to a weighted projective space of the specified weights.
This first block generates the polytope corresponding to our weighted projective space.
[3]:
weights = [1 2 2 2 4];
n = length(weights);
verts = zeros(Int64,n,n+1);
for i = 1:n
verts[i,i] = lcm(weights)/weights[i]
end
P = convexHull(3*verts);
Fᵀ,a = facetRepresentation(P);
polymake: used package ppl
The Parma Polyhedra Library ([[wiki:external_software#PPL]]): A C++ library for convex polyhedra
and other numerical abstractions.
http://www.cs.unipr.it/ppl/
We create a degenerate system \(\hat{f}\) below. The degeneracy comes from solutions lying on the intersection of divisors \(D_5\cap D_6\).
[4]:
k = n+1;
@polyvar x[1:k] t[1:n];
latpts = getLatticePoints(P,x);
mons = [prod(t.^latpts[ℓ,:]) for ℓ=1:size(latpts,1)];
M5 = (Fᵀ[5,:]'*latpts')[:];
M6 = (Fᵀ[6,:]'*latpts')[:];
indsmonsonF5 = findall(ℓ -> ℓ == minimum(M5), M5);
indsmonsonF6 = findall(ℓ -> ℓ == minimum(M6), M6);
indsmonsonF56 = intersect(indsmonsonF5,indsmonsonF6);
indsmonsnotonF56 = setdiff(1:length(mons),indsmonsonF56);
g = convert(Array{ComplexF64},rand(1:10,length(indsmonsonF56)))'*mons[indsmonsonF56];
f̂ = [convert(Array{ComplexF64},rand(1:10,length(mons)))'*mons for ℓ=1:n-3];
f̂ = vcat([g + convert(Array{ComplexF64},rand(1:10,length(indsmonsnotonF56)))'*mons[indsmonsnotonF56] for i = 1:3],f̂);
We perturb the degenerate system \(\hat{f}\) to move all solutions to the torus.
[5]:
ε = 1e-7
for i = 1:3
f̂[i] = f̂[i] + ε*exp.(randn(length(mons))*im)'*mons
end
We solve the system using the Cox homotopy.
[6]:
@time homSols, f, toricSols, homTargetResult = coxHomotopy(f̂, P, Fᵀ, a);
Tracking 7776 paths... 100%|████████████████████████████| Time: 0:05:19
# paths tracked: 7776
# non-singular solutions (real): 7776 (0)
# singular endpoints (real): 0 (0)
# total solutions (real): 7776 (0)
1332.423907 seconds (263.71 M allocations: 22.131 GiB, 0.75% gc time)
polymake: used package cdd
cddlib
Implementation of the double description method of Motzkin et al.
Copyright by Komei Fukuda.
http://www-oldurls.inf.ethz.ch/personal/fukudak/cdd_home/
Here’s a plot of the magnitude of the computed solutions.
[7]:
using PyPlot
maxcoords = [maximum(abs.(sol)) for sol ∈ toricSols]
semilogy(sort(maxcoords),"bo")
xlabel("solution index");
ylabel("solution norm");
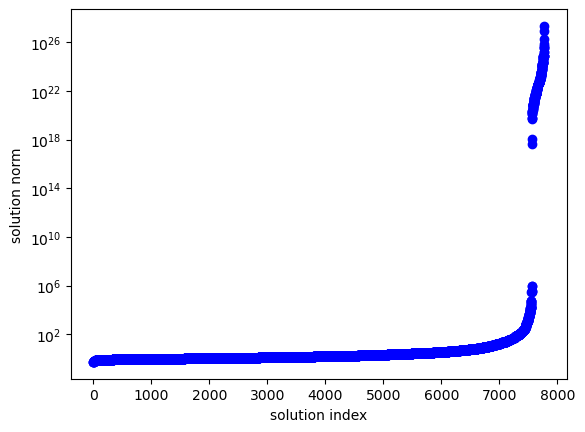
All computed solutions (including the large ones) have a small backward error.
[8]:
residuals = get_residual(f̂,toricSols,t)
semilogy(residuals,"ro")
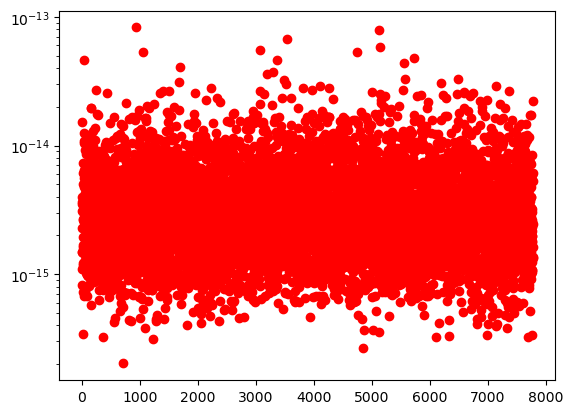
[8]:
1-element Array{PyCall.PyObject,1}:
PyObject <matplotlib.lines.Line2D object at 0x1777fe610>
Due to premature truncation of seemingly diverging paths, the standard polyhedral homotopy misses about 200 solutions.
[9]:
solve(f̂)
Tracking 7776 paths... 100%|████████████████████████████| Time: 0:04:05
# paths tracked: 7776
# non-singular solutions (real): 7561 (24)
# singular endpoints (real): 0 (0)
# total solutions (real): 7561 (24)
[9]:
Result with 7561 solutions
==========================
• 7776 paths tracked
• 7561 non-singular solutions (24 real)
• random_seed: 0xf28bb5a0
• start_system: :polyhedral
[10]:
length(findall(r->r<1e-10,residuals))
[10]:
7776
[ ]:
nruns = 10
nsols_HC_list = []
for ℓ = 4:16
resℓ = []
for s = 1:nruns
k = n+1;
@polyvar x[1:k] t[1:n];
latpts = getLatticePoints(P,x);
mons = [prod(t.^latpts[ℓ,:]) for ℓ=1:size(latpts,1)];
M5 = (Fᵀ[5,:]'*latpts')[:];
M6 = (Fᵀ[6,:]'*latpts')[:];
indsmonsonF5 = findall(ℓ -> ℓ == minimum(M5), M5);
indsmonsonF6 = findall(ℓ -> ℓ == minimum(M6), M6);
indsmonsonF56 = intersect(indsmonsonF5,indsmonsonF6);
indsmonsnotonF56 = setdiff(1:length(mons),indsmonsonF56);
g = convert(Array{ComplexF64},rand(1:10,length(indsmonsonF56)))'*mons[indsmonsonF56];
f̂ = [convert(Array{ComplexF64},rand(1:10,length(mons)))'*mons for ℓ=1:n-3];
f̂ = vcat([g + convert(Array{ComplexF64},rand(1:10,length(indsmonsnotonF56)))'*mons[indsmonsnotonF56] for i = 1:3],f̂);
ε = 10.0^(-ℓ)
for i = 1:3
f̂[i] = f̂[i] + ε*exp.(randn(length(mons))*im)'*mons
end
#@time homSols, f, toricSols, homTargetResult = coxHomotopy(f̂, P, Fᵀ, a);
R = solve(f̂)
residuals_HC = get_residual(f̂,solutions(R),t)
nsols_HC = length(findall(r->r<1e-10,residuals_HC))
push!(resℓ,nsols_HC)
end
push!(nsols_HC_list,sum(nsols_HC)/nruns)
end
nsols_HC_list
Tracking 7776 paths... 10%|██▉ | ETA: 0:03:38
# paths tracked: 813
# non-singular solutions (real): 812 (0)
# singular endpoints (real): 0 (0)
# total solutions (real): 812 (0)
[ ]: