S-EPGP demo
Imports, etc
[1]:
## Imports
import torch
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from pde import CartesianGrid, solve_laplace_equation
# Get cpu or gpu device for training.
device = "cuda" if torch.cuda.is_available() else "cpu"
torch.set_default_dtype(torch.float64)
torch.manual_seed(13);
True solution
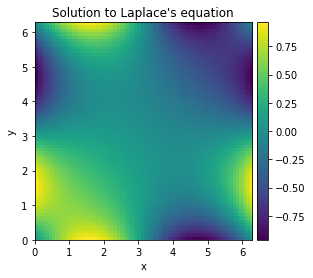
We compute a numerical solution to the Laplace equation in 2D: \(\partial_x^2 + \partial_y^2 = 0\).
[2]:
grid = CartesianGrid([[0, 2 * np.pi]] * 2, 64)
bcs = [{"value": "sin(y)"}, {"value": "sin(x)"}]
res = solve_laplace_equation(grid, bcs)
res.plot();
We convert the py-pde types to PyTorch tensors
[3]:
Ps = torch.tensor(grid.cell_coords)
u_true = torch.tensor(res.data)
Learning data will consist of randomly sampled points in the numerical solution
[4]:
train_pts = 50
train_idx = torch.randperm(len(u_true.flatten()))[:train_pts]
X = Ps.flatten(0,1)[train_idx]
U = u_true.flatten()[train_idx]
Setting up a S-EPGP kernel
Running the command solvePDE in Macaulay2 reveals two varieties, namely the lines $ a = i b$ and \(a = - i b\), where \(a,b\) are spectral variables corresponding to \(x,y\) respecively. For both lines, there is only one Noetherian multiplier, namely 1. This means that the Ehrenpreis-Palamodov representation of solutions to Laplace’s equations are of the form
By parametrizing the two lines, we can rewrite the integrals in a simpler form. We use the parametrizations
The integrals then become
We approximate each measure with \(m\) Dirac delta measures. This translates to the S-EPGP kernel
where \(\Phi(x,y)\) is the vector with entries
and \(\Sigma\) is a \(2m \times 2m\) diagonal matrix with positive entries \(\sigma_j^2\).
Our goal will be to learn the \(c_j \in \mathbb C, \sigma_j^2 > 0\) that minimize the log-marginal likelihood.
Given an array c of length 2m and a s × 2 matrix X of points (x,y), the function Phi returns the 2m × s matrix with columns \(\Phi(x,y)\).
[5]:
def Phi(c,X):
c1, c2 = c.chunk(2)
c1 = c1.unsqueeze(1) * torch.tensor([1+1.j,1-1.j])
c2 = c2.unsqueeze(1) * torch.tensor([1-1.j,1+1.j])
cc = torch.cat([c1,c2])
return cc.inner(X).exp()
Objective function
Suppose we are trying to learn on \(s\) data points. Let \(X\) be the \(s \times 2\) matrix with input points \(x_k, y_k\), and \(U\) the \(s \times 1\) vector with output values \(u_k\). Let \(\Phi\) be the \(2m \times s\) matrix of features obtained by the function Phi above.
The negative log-marginal likelihood function is
where \(\sigma_0^2\) is a noise coefficient, and
This can be computed efficiently using a Cholesky decomposition: \(A = LL^H\). Ignoring constants and exploiting the structure of \(\Sigma\), we get the objective function
The function below computes the Negative Log-Marginal Likelihood (NLML). Here we assume that Sigma is a length \(2m\) vector of values \(\log \sigma_j^2\), and sigma0 is \(\log \sigma_0^2\)
[6]:
def NLML(X,U,c,Sigma,sigma0):
phi = Phi(c,X)
A = phi @ phi.H + torch.diag_embed((sigma0-Sigma).exp())
L = torch.linalg.cholesky(A)
alpha = torch.linalg.solve_triangular(L, phi @ U, upper=False)
nlml = 1/(2*sigma0.exp()) * (U.norm().square() - alpha.norm().square())
nlml += (phi.shape[1] - phi.shape[0])/2 * sigma0
nlml += L.diag().real.log().sum()
nlml += 1/2 * Sigma.sum()
return nlml
Training
We now set up parameters, initial values, optimizers and the training routine. We will use \(m = 8\) Dirac delta measures for each integral.
[7]:
m = 8
Sigma = torch.full((2*m,), -np.log(2*m)).requires_grad_()
sigma0 = torch.tensor(np.log(1e-5)).requires_grad_()
c = (1*torch.randn(2*m, dtype=torch.complex128)).requires_grad_()
U = U.to(torch.complex128).reshape(-1,1)
X = X.to(torch.complex128)
[8]:
def train(opt, sched, epoch_max = 1000):
for epoch in range(epoch_max):
nlml = NLML(X,U,c,Sigma,sigma0)
print(f'Epoch {epoch+1}/{epoch_max}\tNLML {nlml.detach():.3f}\tsigma0 {sigma0.exp():.3}\tc std {c.std():.3f}\tlr {sched.get_last_lr()[0]}', end='\r')
opt.zero_grad()
nlml.backward()
opt.step()
sched.step()
Here we use a simple Adam optimizer, with learning rate 0.1, and decaying by a factor of 10 every 1000 steps. We train for 3000 epochs.
[9]:
opt = torch.optim.Adam([c,Sigma,sigma0], lr = 1e-2)
sched = torch.optim.lr_scheduler.StepLR(opt,3000,gamma=0.1)
train(opt,sched,3000)
Epoch 3000/3000 NLML -232.572 sigma0 7.4e-06 c std 0.695 lr 0.011
Prediction
Suppose we want to use our trained model to predict the value of the function at \(r\) points \((x,y)\), organized in the \(r \times 2\) matrix \(X_*\). We will do inference using the posterior mean, which is given by
where \(\Phi_*\) is the \(2m \times r\) matrix, with columns \(\Phi(x,y)\) for each row in \(X_*\).
The following function computes the prediction, where the variable X_ corresponds to \(X_*\)
[10]:
def predict(X_, X,U,c,Sigma,sigma0):
with torch.no_grad():
phi = Phi(c,X)
A = phi @ phi.H + torch.diag_embed((sigma0-Sigma).exp())
L = torch.linalg.cholesky(A)
alpha = torch.linalg.solve_triangular(L, phi @ U, upper=False)
alpha1 = torch.linalg.solve_triangular(L.H, alpha, upper=True)
phi_ = Phi(c,X_)
return (phi_.H @ alpha1).real
[11]:
X_ = Ps.flatten(0,1).to(torch.complex128)
u_pred = predict(X_, X, U, c, Sigma, sigma0)
The root mean square error of our prediction is below
[12]:
(u_pred.view_as(u_true) - u_true).square().mean().sqrt().item()
[12]:
0.0003669123836532972
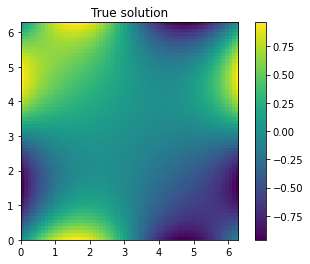
We can also visually compare the true solution with our prediction. The true solution is
[13]:
ax = plt.imshow(u_true,extent=2*[0,2*np.pi])
plt.colorbar(ax)
plt.title("True solution");
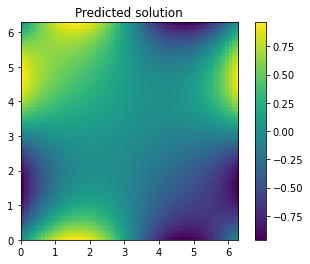
[14]:
ax = plt.imshow(u_pred.view_as(u_true),extent=2*[0,2*np.pi])
plt.colorbar(ax)
plt.title("Predicted solution");
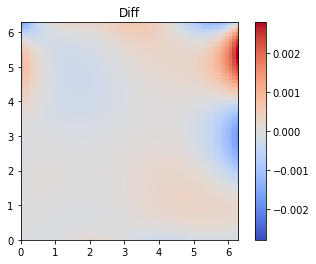
Finally, we plot the difference between the true and predicted solutions
[15]:
diff = u_pred.view_as(u_true) - u_true
limit = max(diff.max(), -diff.min())
ax = plt.imshow(diff,extent=2*[0,2*np.pi], cmap='coolwarm', vmin = -limit, vmax = limit)
plt.colorbar(ax)
plt.title("Diff");