Graph Curve Matroids

This page contains auxiliary files to the paper:
Alheydis Geiger, Kevin Kühn, and Raluca Vlad: Graph Curve Matroids
arXiv: https://arxiv.org/abs/2311.08332

Abstract: We introduce a new class of matroids, called graph curve matroids. A graph curve matroid is associated to a graph and defined on the vertices of the graph as a ground set. We prove that these matroids provide a combinatorial description of hyperplane sections of degenerate canonical curves in algebraic geometry. Our focus lies on graphs that are 2-connected and trivalent, which define identically self-dual graph curve matroids, but we also develop extensions. Finally, we provide an algorithm that computes the graph curve matroid associated to a given graph, as well as an implementation and data of examples that can be used in Macaulay2.

Constructing the graph curve matroid

We have implemented the algorithm for computing the graph curve matroid of any given graph in Macaulay2. The code can be downloaded here graphCurveMatroid.m2.

Please note that this code only works for simple graphs, as \(\texttt{Macaulay2}\) does not work with parallel edges in graphs. However, one can still construct the graph curve matroid of a non-simple graph, but the code needs some adaptation. The main functionalities that need modification are the computation of the cycle matroid, which works for graphs with loops but without parallel edges, and the computation of the set of incident edges \(\delta(A)\) for a vertex set \(A\), which in the above code is implemented only for simple graphs.

Here is an example how to use the code in Macaulay2 for a simple graph:

value get "graphCurveMatroid.m2";

G = graph({{1, 2}, {2, 3}, {3, 1}, {3, 5}, {4, 5}, {4, 2}, {5, 7}, {6, 7}, {6, 4}, {7, 8}, {8, 6}, {1, 8}}, EntryMode => "edges");

M = graphCurveMatroid G;

M == dual(M)
true

rank M
4

#bases M
54

#circuits M
26

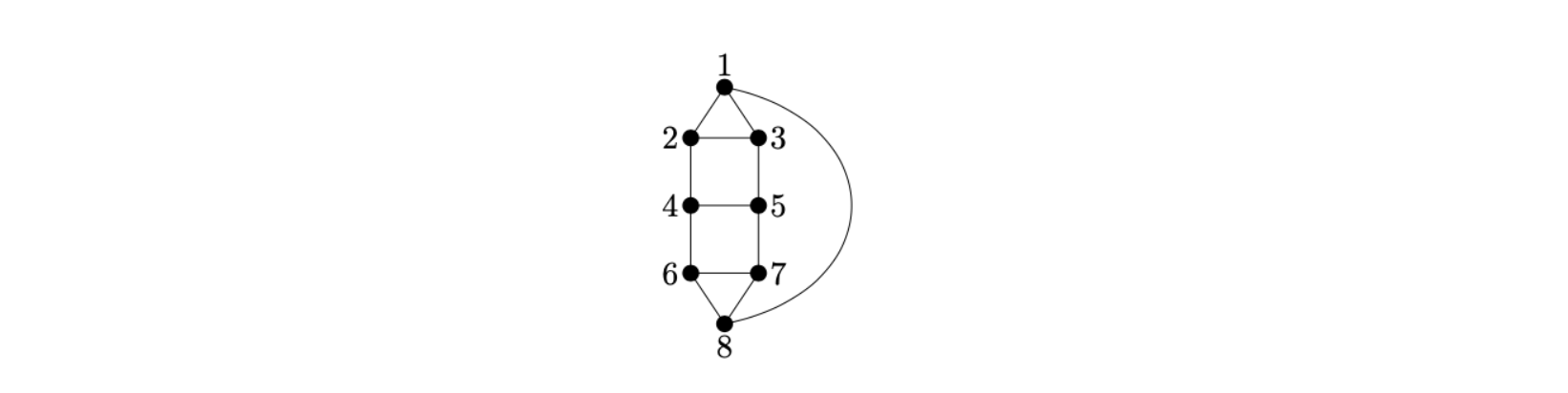
The figure displays the double house graph from Figure 2 in the paper with the labeling as used to make the graph \(\texttt{G}\) in the code example. So the corresponding graph curve matroid for the double house graph is identically self-dual of rank 4, has 54 bases and 26 circuits.

Runtime of the algorithm

The runtime of the algorithm to compute the graph curve matroid grows exponentially with the number of vertices of the graph. For example, the computation of a graph curve matroid of a trivalent graph with 14 vertices takes already 1673.56 seconds.

Graphs and their graph curve matroids

The data on trivalent (also called cubic) simple graphs originated here https://houseofgraphs.org/meta-directory/cubic.

Below, we provide the edge sets for trivalent simple graphs with up to 12 vertices and files with the bases of the associated graph curve matroids in a Macaulay2 readable format.

Graphs

graphs_04vertices.txt
graphs_06vertices.txt
graphs_08vertices.txt
graphs_10vertices.txt
graphs_12vertices.txt

Graph Curve Matroids

matroids_graphs_04vertices.txt
matroids_graphs_06vertices.txt
matroids_graphs_08vertices.txt
matroids_graphs_10vertices.txt
matroids_graphs_12vertices.txt

How to use the files: The graph arising from the edges in the ith entry of the list in graphs_04vertices.txt gives rise to the graph curve matroid given by the set of bases stored in the ith entry of the list in matroids_graphs_04vertices.txt.

value get "graphCurveMatroid.m2";

GraphsList = value get "graphs_06vertices.txt";

#GraphsList
2

G = graph(GraphsList#0, EntryMode =>"edges"); --build a graph from the first list of edges

MatroidsList = value get "matroids_graphs_06vertices.txt";

M = matroid({0,1,2,3,4,5}, MatroidsList#0, EntryMode => "bases") --build a matroid from the list of bases

M == graphCurveMatroid G;
true

Constructing a basis

Given a trivalent, 2-connected graph \(G\) and a vertex \(v\), the proof of Proposition 4.3 provides a constructive way to directly create a basis of \(M_G\) containing \(v\) without computing the whole matroid \(M_G\) first. Correctness follows from Lemmas 4.1 and 4.2.

We implemented this algorithm in Macaulay2. Our code can be downloaded here: basis-construction.m2. The code asks the user to input a graph (in a Macaulay2-readable format) and a vertex, and outputs to the user a basis of the associated graph curve matroid containing the given vertex.

value get "basis-construction.m2"
Graph: graph({{1, 2}, {2, 3}, {3, 1}, {3, 5}, {4, 5}, {4, 2}, {5, 7}, {6, 7}, {6, 4}, {7, 8}, {8, 6}, {1, 8}}, EntryMode => "edges")
vertex: 3
set {1, 3, 5, 7}

Project page created: 08/11/2023

Project contributors: Alheydis Geiger, Kevin Kühn, and Raluca Vlad

Corresponding author of this page: Alheydis Geiger, geiger@mis.mpg.de

Code written by: Alheydis Geiger and Raluca Vlad

Software used: Macaulay2 (v1.19.1)

System setup used: MacBook Pro with macOS 12.7, Processor 2,6 GHz Quad-Core Intel Core i7, Memory 16 GB, Graphics Intel HD Graphics 530.

License for code of this project page: MIT License (https://spdx.org/licenses/MIT.html)

License for all other content of this project page (text, images, …): CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/)

Last updated 09/07/2024.