Chapter 7: Tropical Algebra

This chapter was presented by Yassine El Maazouz and Rodica Dinu. All their codes are in Polymake.

Here is an example of computing the tropical determinant using polymake. First you need to specify that you want to use the “tropicak” by typing:

application "tropical";
$A = new Matrix<TropicalNumber<Min>>([[1,2,3],[1,2,4],[1,0,1]]);
print tdet($A); ## Value // computes using the Hungarian algorithm
print tdet_and_perm($A); # Value and optimal permutation

You can define a tropical polynomial and visualize its hypersurface:

$P = toTropicalPolynomial("min(3*w, 1 - 2*w - x, 1- 2*w - y, 1 - 2*w -z, 3 - w - x -y, 3 - w - x -x, 3 - w -y -z, 6 -x -y -z)");
$V = new Hypersurface<Min>(POLYNOMIAL=>$P);
$V->VISUAL;
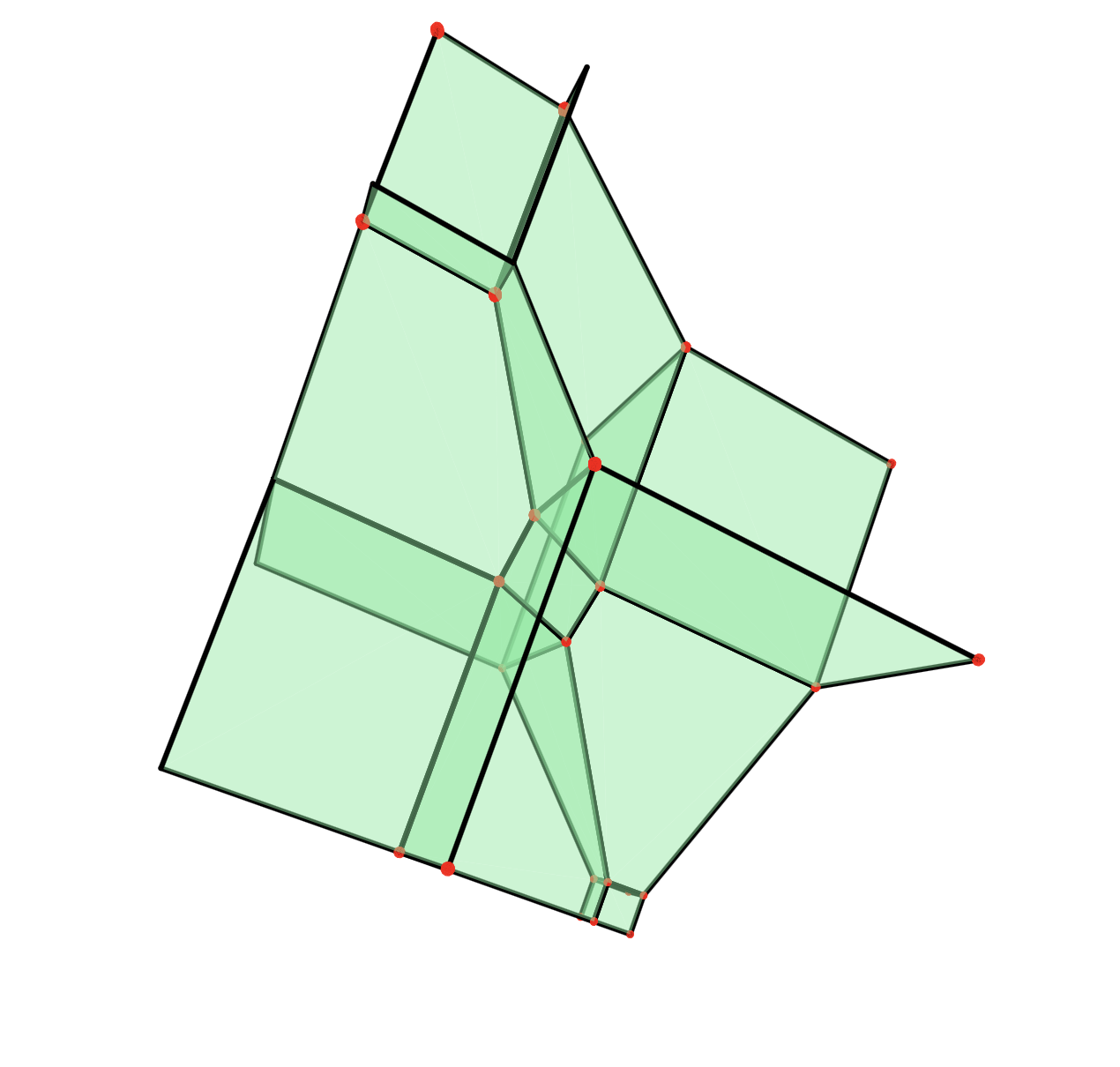
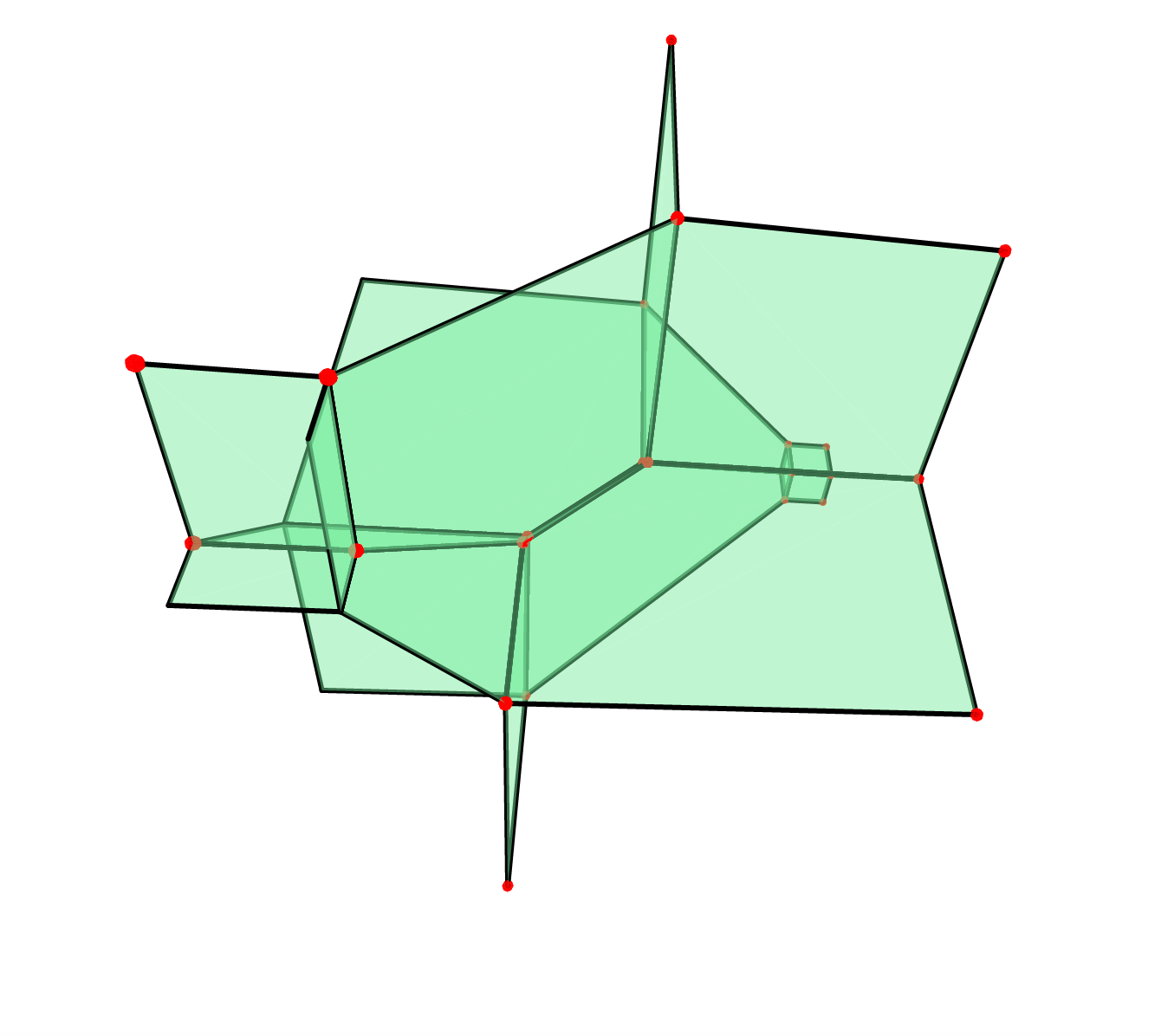
../_images/trop1.png ../_images/trop2.png

you can do all sorts of things in polymake like compute regular subdivision and tropical polytopes. (you should try it out!!)

$Polytope = new Polytope<Min>(POINTS=>[[0,1,1],[1,0,1],[1,1,0]]);
$Polytope->VISUAL;
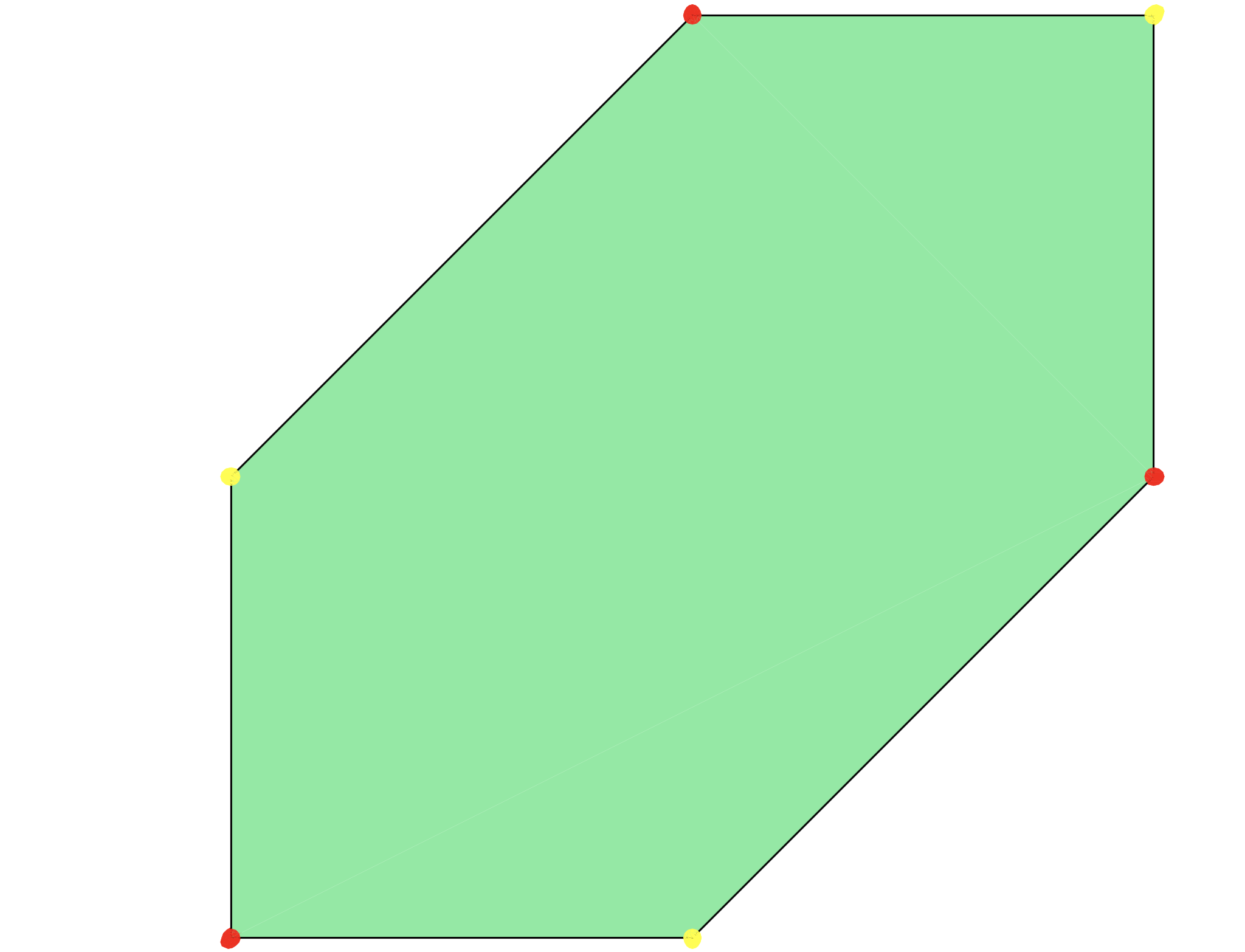
../_images/trop3.png

Here you see that the tropical image of a linear map is not a linear tropical space as one might expect. For more details and cool computations please check the tropical application user guide on polymake.org.