Solving Equations Using Khovanskii Bases
ABSTRACT: We develop a new eigenvalue method for solving structured polynomial equations over any field. The equations are defined on a projective algebraic variety which admits a rational parameterization by a Khovanskii basis, e.g., a Grassmannian in its Plücker embedding. This generalizes established algorithms for toric varieties, and introduces the effective use of Khovanskii bases in computer algebra. We investigate regularity questions and discuss several applications.
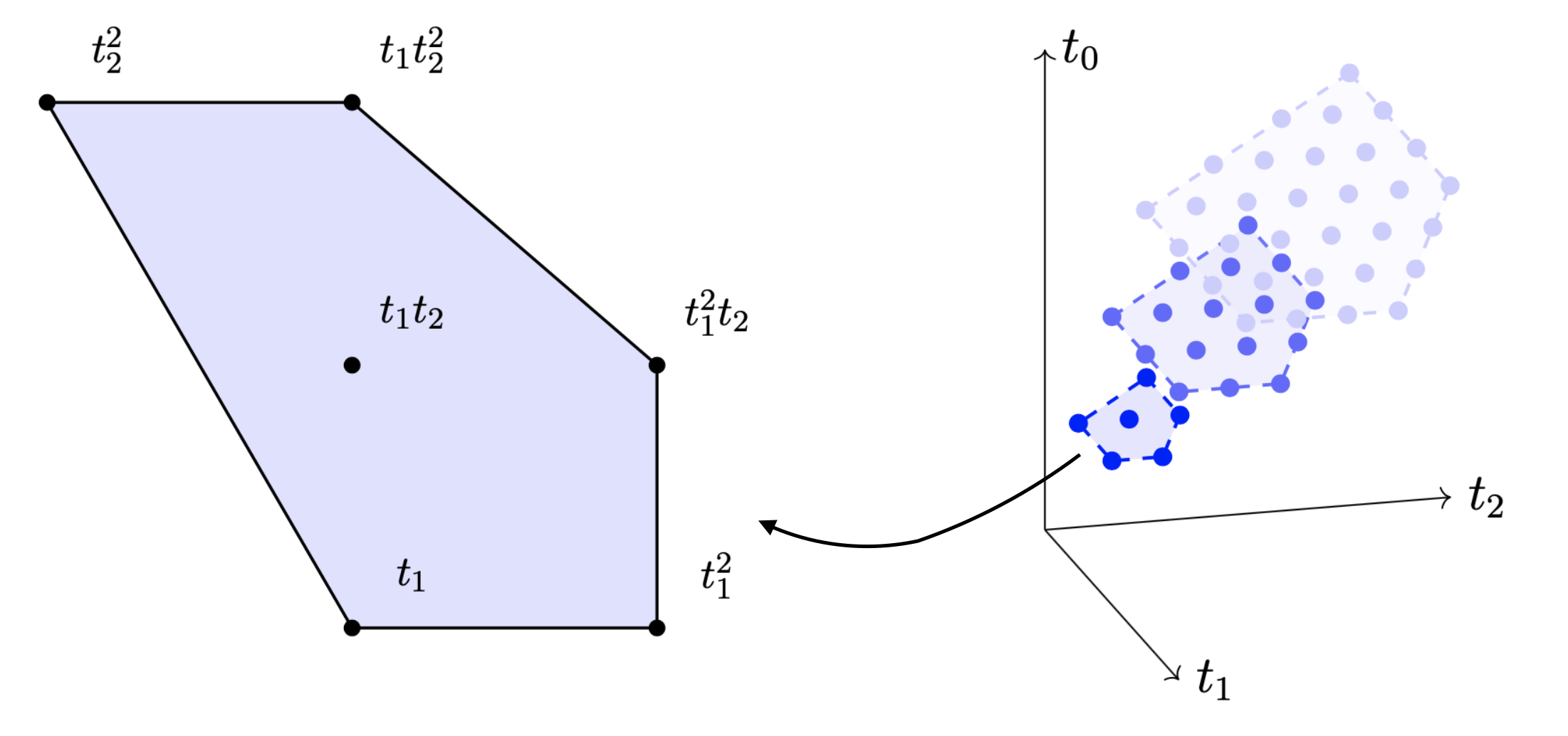
The picture below represents the initial algebra of the Del Pezzo surface in Example 2.6 in the paper.
Our eigenvalue method is implemented in julia. The package is called KhovanskiiSolving.jl. It makes use of Oscar.jl (v0.12.1).
Our Julia code can be downloaded here KhovanskiiSolving_Julia_code.zip.
All the examples computed and discussed in the paper can be reproduced using this code, and they can be downloaded here Examples_KhovanskiiSolving.zip.
The following tables report the computations performed over the Grassmannians Gr(3,6) and Gr(2,4).

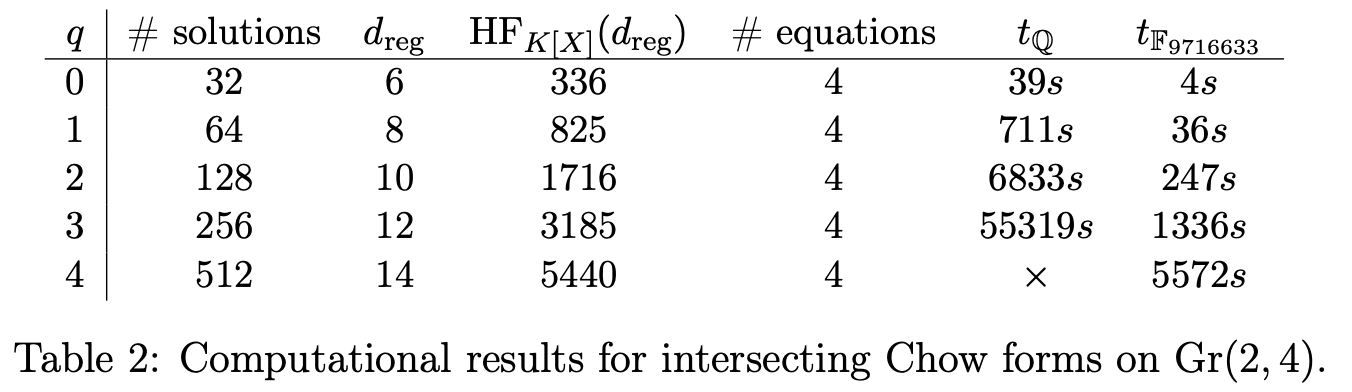
The code in julia used for creating Table 1 and Table 2 can be downloaded here Table1_Gr36_code.jl, Table2_Gr24_code.jl .
Project page created: 23/06/2023
Project contributors: Barbara Betti, Marta Panizzut, Simon Telen
Corresponding author of this page: Barbara Betti, email betti@mis.mpg.de
Software used: Julia (Version 1.9).
License for code of this project page: MIT License https://spdx.org/licenses/MIT.html.