Introduction

We present the matrix \(A(\Sigma)\) and its kernel \(H(\Sigma)\), as both play an important role in our computations.

In our paper we study parameter identifiability of Graphical Continuous Lyapunov Models. Recall that every graph induces a statistical model (Definition 1.3). Identifiability then corresponds to the existence of a unique solution to the Lyapunov equation \(M \Sigma + \Sigma M^{\top}=-C\) for a support restricted matrix \(M \in \mathrm{Stab}(E)\), where \(E\) is the edge set of the graph \(G=(V,E)\) under consideration. For more details consider Definition 2.1. In general, the matrix \(C\) is assumed to be positive-definite. However, we obtain our strongest results when focusing on \(C\) diagonal. We give more details in our paper. Vectorizing the Lyapunov equation, we obtain the linear equation system \(A(\Sigma) \mathrm{vec}(M)=-\mathrm{vech}(C)\). We display the matrix \(A(\Sigma)\) for \(p=3\) nodes.

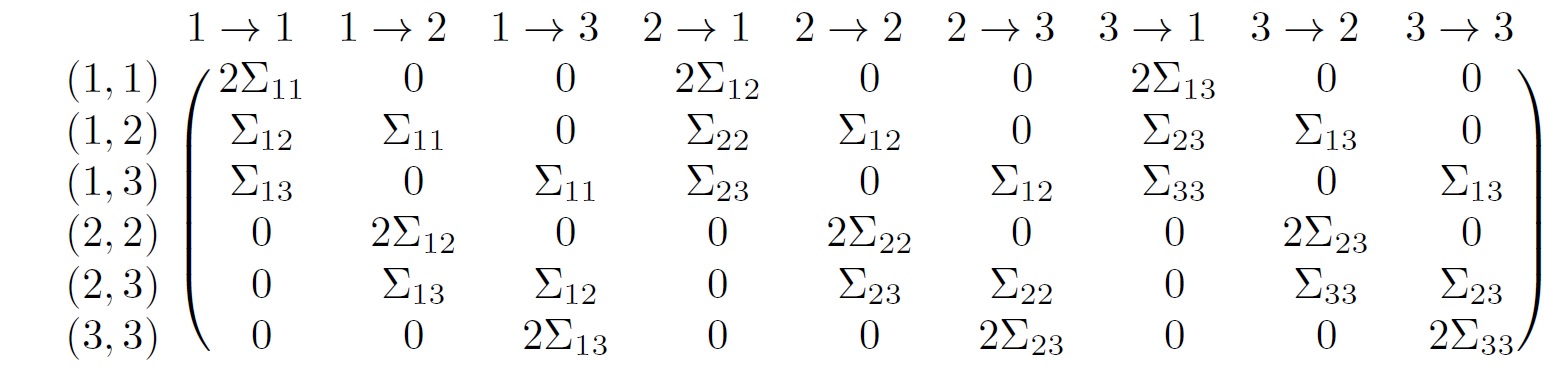
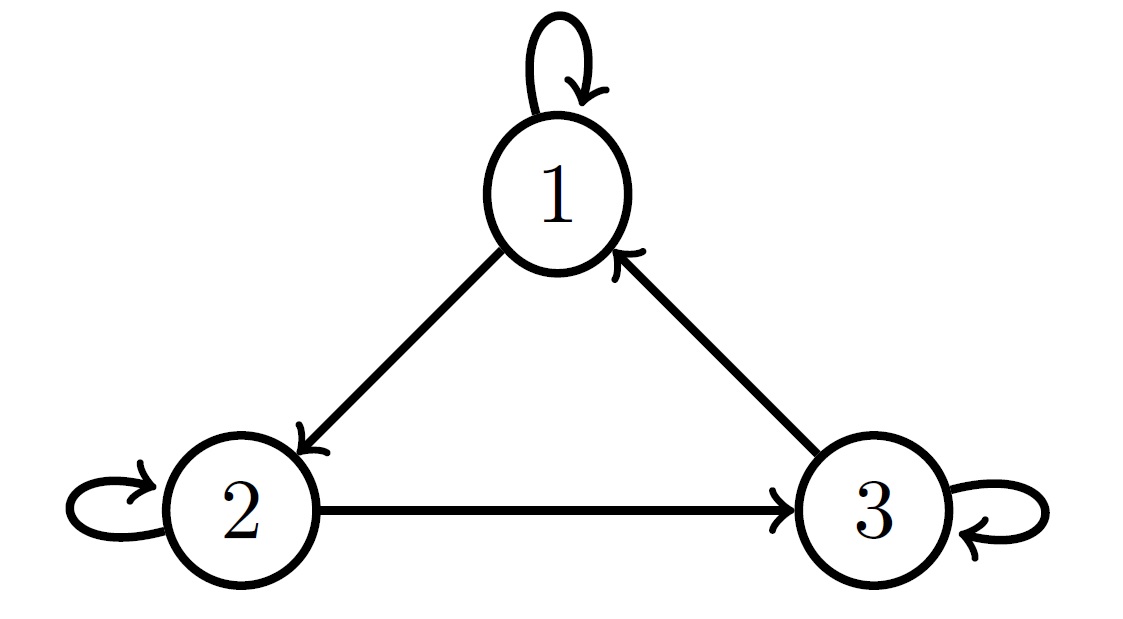
The matrix has only \((p+1)p/2=(3+1)3/2=6\) rows due to the symmetry of the Lyapunov equation. The column indices correspond to possible edges in a graph on 3 nodes. In Lemma 3.3. we present a necessary and sufficient criterion for identifiability based on the (full) column rank of \(A(\Sigma)_{\cdot,E}\). By \(A(\Sigma)_{\cdot,E}\) we denote the submatrix of \(A(\Sigma)\) consisting of the columns with indices that are elements of the edge set \(E\). For illustration, we consider the 3-cycle

Then we obtain

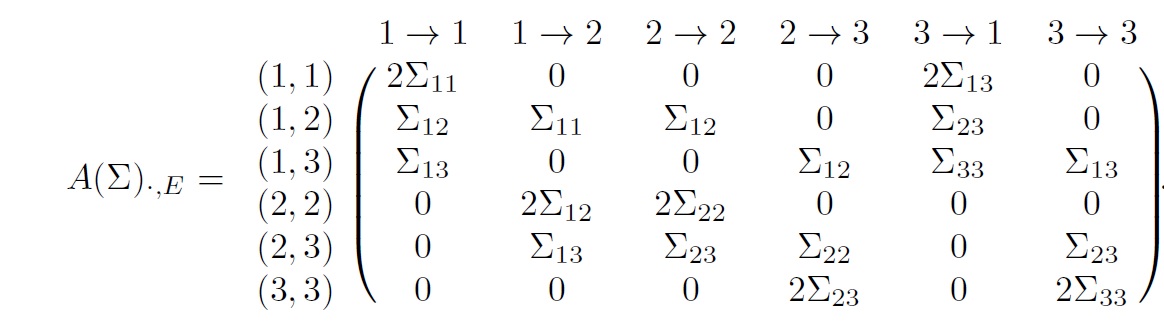
In Macaulay2 these two matrices can be obtained with the following lines of code. It requires downloading LyapunovModel.

restart
loadPackage "LyapunovModel"
G=digraph {{1,2},{2,3},{3,1}}
A=ASigma G
AS=ASigmaGraph G

Calculating the determinant we obtain \(\det(A(\Sigma)_{\cdot,E})=2^3 \det(\Sigma) (\Sigma_{11}\Sigma_{22}\Sigma_{33}-\Sigma_{12}\Sigma_{13}\Sigma_{23})\). Of course, \(\det(\Sigma)>0\) and, as we show in Example 1.5, the same applies to the second factor. Using the duality of \(A(\Sigma)\) and its kernel \(H(\Sigma)\), the rank conditions in Lemma 3.3 can also be established in terms of the kernel, as we present in Lemma 5.4. In case of a complete graph (\((p+1)p/2\) edges), this leads to a convenient reduction of the problem size. For \(p=3\) nodes we obtain

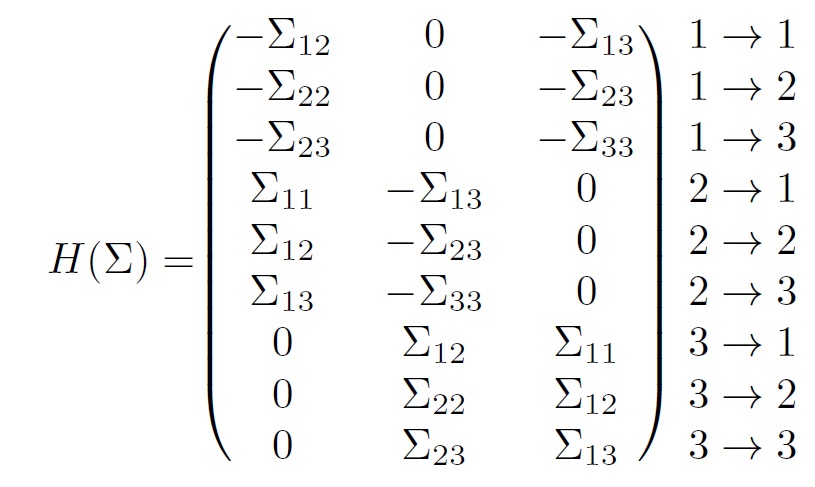
Contrary to \(A(\Sigma)\), we have to select the non-edges of the graph to obtain the relevant matrix \(H(\Sigma)_{E^c,\cdot}\). Returning to the 3-cycle example and calculating the determinant, we obtain the same critical factor as before

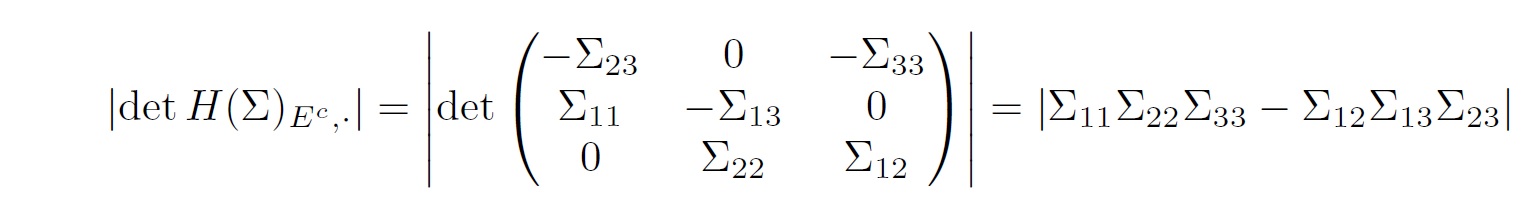
We can compute the restricted kernel and its determinant using this Macaulay2 code.

--compute kernel
kern=syz A
--compute restricted kernel corresponding to non-edges
kernE=kern^(kernelPattern G)
f=det E