Global Identifiability of Simple Cyclic Graphs
We present Macaulay2 sessions proving that \(A(\Sigma)_{\cdot,E}\) is full rank for every \(\Sigma \in \mathrm{PD}_p\)
for almost all \(G=(V,E)\) complete and up to \(p=5\) nodes. This does not only prove global identifiability, but also that \(\mathcal{M}_{G,C}=\mathrm{PD}_p\), see Corollary 4.4.
Proposition 2.6. and Proposition 2.8. show that global identifiability is inherited by the subgraphs of a gloabally identifiable graph.
The direct approach using \(A(\Sigma)\) can be found in SimpleCyclicASigma and the approach using the kernel \(H(\Sigma)\) can be found in
SimpleCyclicKernel. Both require downloading LyapunovModel.
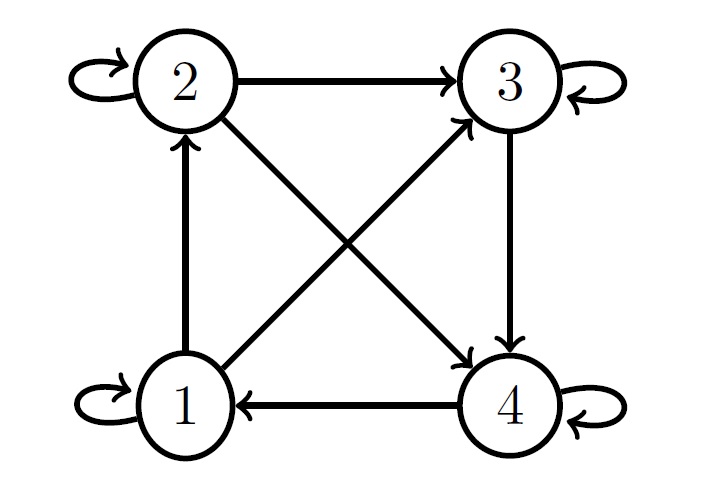
We illustrate the computations using the graph in Example 5.1. The graph is a completion of the 4-cycle such that \(|E|=p(p+1)/2\) and is displayed below.
Using the Cholesky decomposition of \(\Sigma=LL^{\top}\), we factor \(\det A(\Sigma)\).
-- Completion of 4-cycle, ASigma --
restart
loadPackage "LyapunovModel"
-- completion of the 4-cycle
G=digraph {{1, 2}, {1, 3}, {2, 3}, {2, 4}, {3, 4}, {4, 1}}
(R,M,SL,S)=lyapunovDataPD G
AS=ASigmaGraphPD(G)
F=extractFactors(factor det AS) --factors det AS
netList F
Some factors, as the determinant of the positive-definite \(\Sigma\), are obviously non-vanishing. For the critical factor we compute the SOS decomposition, list the generators and search for one that is non-negative due to the positive-definiteness of \(\Sigma\). In this example, it is \(l_{2,2} l_{3,3} l_{4,4}>0\).
--SOS decomposition of relevant factor of the determinant
F_4
loadPackage "SemidefiniteProgramming"
loadPackage "SumsOfSquares"
sol=solveSOS F_4
s=sosPoly sol
netList s#generators
--l_(2,2)l_(3,3)l_(4,4)>0
Alternatively, it is possible to use the kernel to prove global identifiability of the completion of the 4-cycle. We calculate \(\det(H(\Sigma)_{E^c,\cdot})\), which is exactly the critical factor of \(\det(A(\Sigma)_{\cdot,E})\) we observed in the previous code chunk.
-- Completion of 4-cycle, kernel --
--compute restricted kernel
kernE=(syz A)^(kernelPattern G);
f=det kernE;
F=extractFactors factor f;
netList F
F_2
sol=solveSOS F_2
s=sosPoly sol
peek s
netList s#generators
--l_(2,2)l_(3,3)l_(4,4)>0
--Check that it is a proper SOS decomposition
F_2==sum apply(s#generators,s#coefficients,(i,j)->i^2*j)
These examples were computed using Macaulay2, version 1.17, on a Surface Pro (2017) with a 2,6 GHz Intel Core i5-7300U processor and 8 GB.