Orders and Polytropes : Matrix Algebras from Valuations
Abstract: We apply tropical geometry to study matrix algebras over a field with valuation. Using the shapes of min-max convexity, known as polytropes, we revisit the graduated orders introduced by Plesken and Zassenhaus. These are classified by the polytrope region. We advance the ideal theory of graduated orders by introducing their ideal class polytropes. This article emphasizes examples and computations. It offers first steps in the geometric combinatorics of endomorphism rings of configurations in affine buildings.
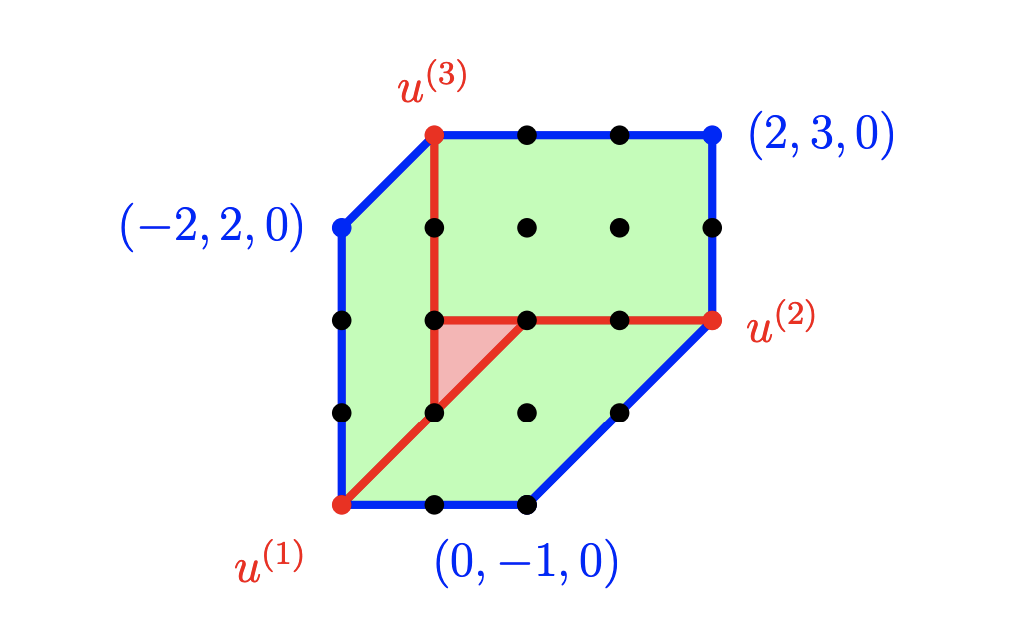
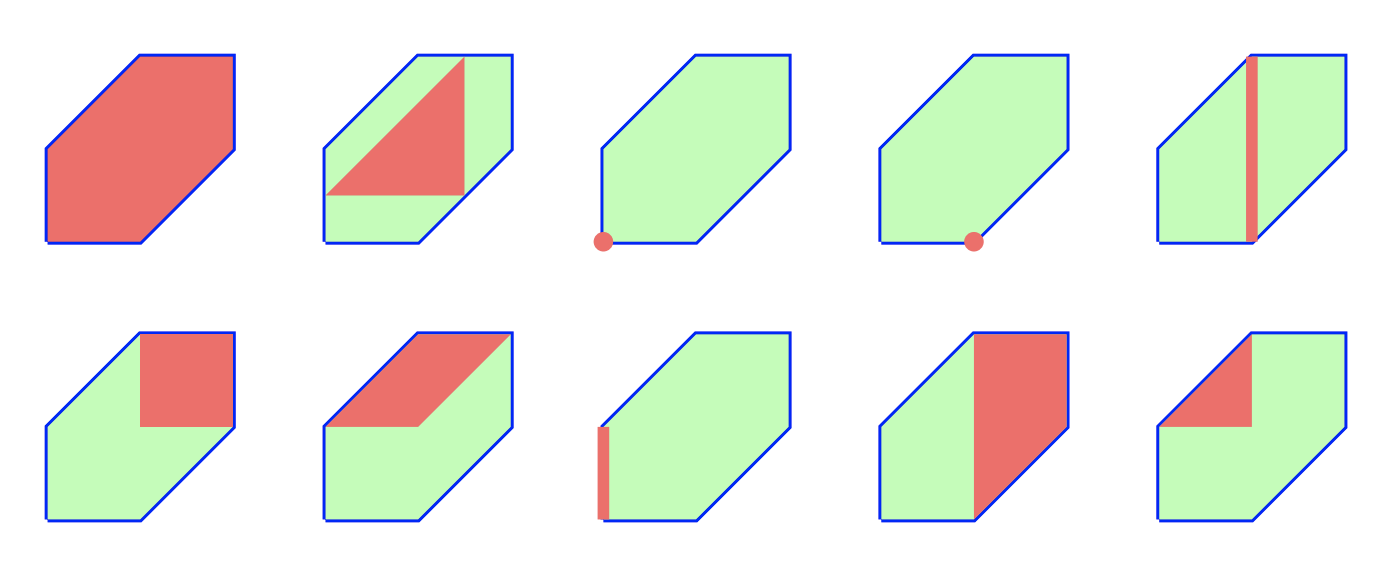
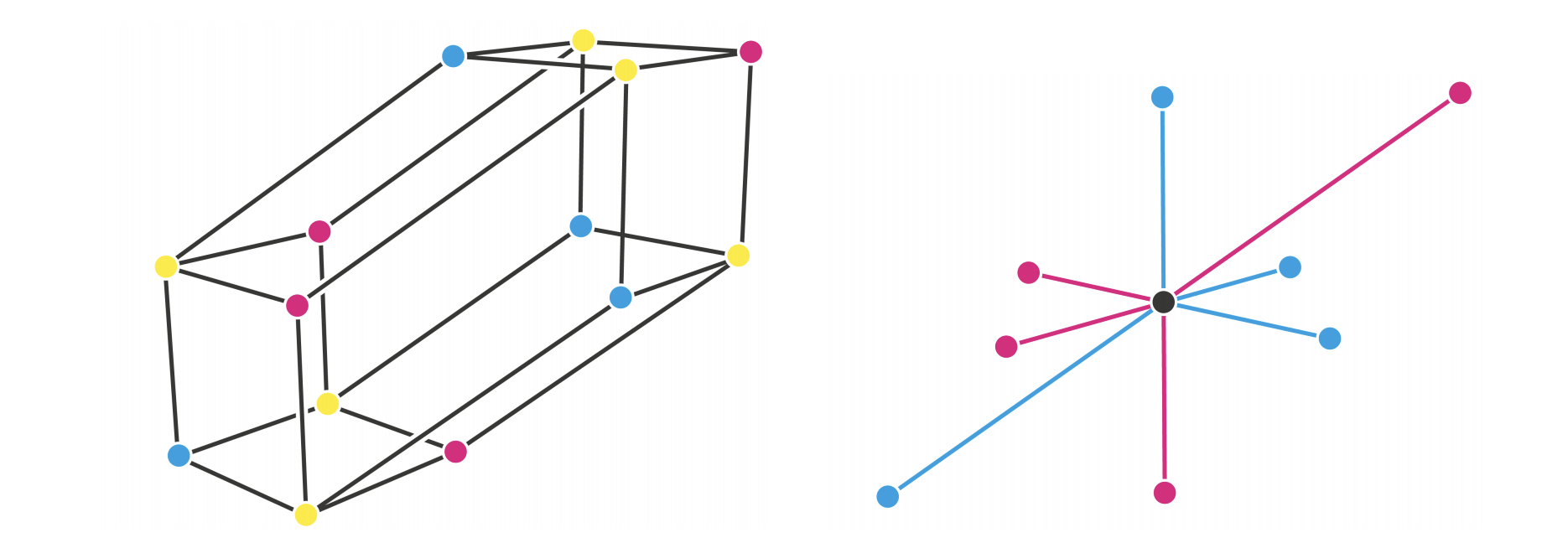
This repository includes our code to compute the polytrope regions \(\mathcal{P}_d\) and truncated polytrope regions \(\mathcal{P}_d(M)\) described in the paper (Section 4). We also provide code to compute the ideal class semigroup \(\mathcal{Q}_M\) and its maximal subgroup \(\mathcal{G}_M\) (Section 5).
Our code is written in Julia (v1.6.2) using the computer algebra system Oscar (v0.5.2).
Please find the following jupyter notebook containing the code:
You can also run our jupyter notebook online:
Project page created: 10/08/2021.
Project contributors: Yassine El Maazouz, Marvin Anas Hahn, Gabriele Nebe, Mima Stanojkovski, Bernd Sturmfels
Corresponding author of this page: Yassine El Maazouz, yassine.el-maazouz@berkeley.edu
Software used: Julia (Version 1.6.2), Oscar (v0.5.2), GAP