The polyhedral type of a polynomial map on the plane.
ABSTRACT: We say that two continuous maps \(f,g:\mathbb{C}^2\to\mathbb{C}^2\) are topologically equivalent if there exist homeomorphisms \(\varphi,\psi:\mathbb{C}^2\to\mathbb{C}^2\) satisfying \(\psi\circ f\circ\varphi = g\). Given any positive integer \(d\), it is known that there are finitely-many topologically non-equivalent polynomial maps \(\mathbb{C}^2\to\mathbb{C}^2\) with given degree \(d\). Due to the lack of systematic methods, the number of these topological types is known only for quadratic maps. In this paper, we describe the topology of generic complex maps on the plane with a given pair of Newton polytopes, and establish a method for constructing topologically non-equivalent maps from pairs of lattice polytopes. We furthermore provide a software implementation of the resulting algorithm, and present lower bounds on the number of topological types for \(d = 3\) and \(d = 4\).
Let \(f:\mathbb{C}^2\to\mathbb{C}^2\) be a polynomial map. We denote by \(C_f = \{\operatorname{det}\operatorname{Jac}_z f=0\}\) the critical locus of \(f\), and by \(D_f = f(C_f)\) the discriminant locus.
By Proposition 2.7, the following quantities are invariant under topological equivalence:
\(\iota_1(f) :\) the topological degree of \(f\).
\(\iota_2(f) :\) the geometric genus of the discriminant locus \(D_f\) of \(f\).
\(\iota_3(f) :\) the Milnor number \(\mu_0(C_f)\) of the critical locus \(C_f\) of \(f\) at the origin.
\(\iota_4(f) :\) the topological multiplicities of the different components of \(D_f\).
\(\iota_5(f) :\) the total number of singularities of the discriminant locus \(D_f\).
Computing the polyhedral type
Let \(A_1, A_2\) be two planar polytopes and \(f = (f_1, f_2):\mathbb{C}^2\to\mathbb{C}^2\) be a generic polynomial map with prescribed Newton polytopes \(\operatorname{Newt}(f_1) = A_1, \operatorname{Newt}(f_2) = A_2.\)
The polyhedral type \(\Psi(A_1, A_2)=(\Psi_1(A_1,A_2),\dots,\Psi_{12}(A_1,A_2))\in\mathbb{Z}^{12}\) of the pair \((A_1, A_2)\) is given in Definition 2.21 in terms of discrete geometry.
By Theorem 2.19, the above invariants \(\iota_1(f), \dots, \iota_5(f)\) are encoded in \(\Psi_1(A_1,A_2), \dots, \Psi_8(A_1,A_2)\) under weak assumptions. We demonstrate this in the following example and showcase our software by computing the polyhedral type \(\Psi(A_1,A_2)\). The meaning of the entries \(\Psi_8(f), \dots , \Psi_{12}(f)\) is also explained in Theorem 2.19.
Example
Consider the map \(f:\mathbb{C}^2\to\mathbb{C}^2\) where
The Newton polytopes \(A_1, A_2\) are of the following shape:
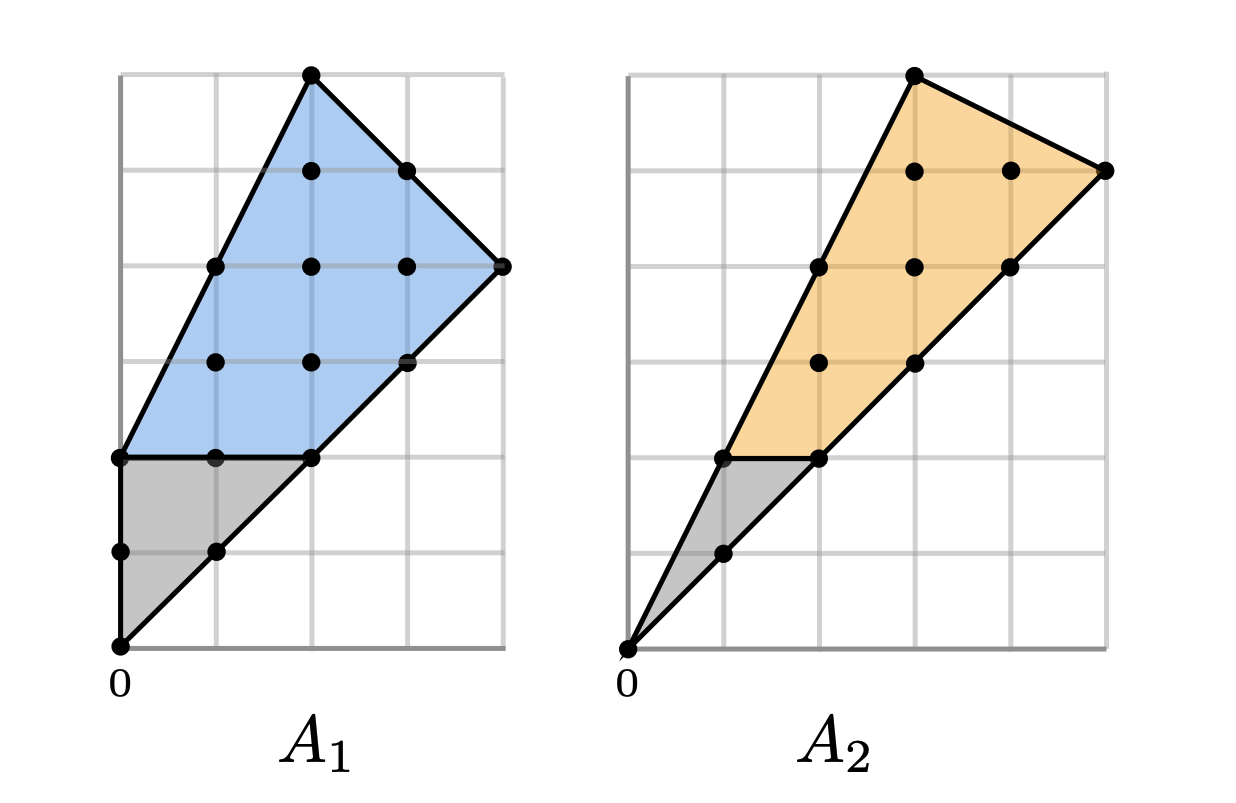
The following Julia code enables our software package:
using Pkg
Pkg.add(url = "https://github.com/kemalrose/PolyhedralTypes.jl")
using PolyhedralTypes
We now compute \(\Psi(A_1, A_2) = (20, 19, 0, 4, 3, 0, 526, 10, 0, 6, 0, 6)\):
A1 = [0 2 4 2; 2 2 4 6];
A2 = [1 2 5 3; 2 2 5 6];
Delta = get_delta(A1, A2);
psi = get_polyhedral_type(A1,A2);
We confirm that:
The topological degree \(\iota_1(f)\) of \(f\) is \(\Psi_1(A_1, A_2) = 20\).
The geometric genus \(\iota_2(f)\) of the discriminant locus \(D_f\) of \(f\) is \(\Psi_2(A_1, A_2) = 19\).
The Milnor number \(\iota_3(f)\) of the critical locus \(C_f\) of \(f\) at the origin is \(\Psi_3(A_1, A_2) = 0\).
\(D_f\) has three components with topological multiplicities \(\iota_4(f) = (1,3,0)\) respectively. These are recorded by \((\Psi_4(A_1, A_2), \Psi_5(A_1, A_2), \Psi_6(A_1, A_2)) = (4,3,0)\), up to permuation, by evaluating elementary symmetric polynomials: \((4,3,0) = (1+3+0, \ 1 \cdot 3 + 0 \cdot 1+0 \cdot 3, \ 0 \cdot 1 \cdot 3 )\).
The total number of singularities on the discriminant locus \(D_f\) is \(\Psi_7(A_1, A_2) = 526\).
Listing planar polytopes
We use software to enumerate all possible Newton polytopes of polynomials of bounded degree. The following command lists the vertices of all \(214946\) polytopes that are contained in the scaled planar simplex \(7\Delta_2\):
pol_List = list_all_polygons(7)
Code
The source code can be downloaded here: PolyhedralTypes.jl.
Project page created: 21/11/2023
Project contributors: Boulos El Hilany and Kemal Rose.
Software used: Julia(Version1.8)
Corresponding author of this page: Kemal Rose, krose@mis.mpg.de.