Quatroids and Rational Plane Cubics
Overview
Abstract. It is a classical result that there are 12 (irreducible) rational cubic curves through 8 generic points in the complex projective plane, but little is known about the non-generic cases. The space of 8-point configurations is partitioned into strata depending on combinatorial objects we call quatroids, a higher-order version of representable matroids. We compute all 779777 quatroids on eight distinct points in the plane, which produces a full description of the stratification. For each stratum, we generate several invariants, including the number of rational cubics through a generic configuration. As a byproduct of our investigation, we obtain a collection of results regarding the base loci of pencils of cubics and positive certificates for non-rationality.
Below, we showcase one illustration of a quatroid together with several of its invariants, in particular the number \(d_{\mathcal Q}\) of rational cubics through a generic configuration which exhibits the specificied linear and quadratic dependencies.
This page archives the code required to compute an exhaustive list of quatroids together with their invariants.
Quatroids.zip– Julia code auxiliary to the article. See the included README file for details.QuatroidsM2Code.zip– Macaulay2 code auxiliary to the article. See the included README file for details.Results.zip– The files generated by the julia and Macaulay2 code.
The following Jupyter notebook shows an example session where the results are produced:
The following two Jupyter notebooks show how to use the Quatroids
julia package with examples. The notebooks can also be downloaded
here: Quatroid66.ipynb, Quatroid97.ipynb.
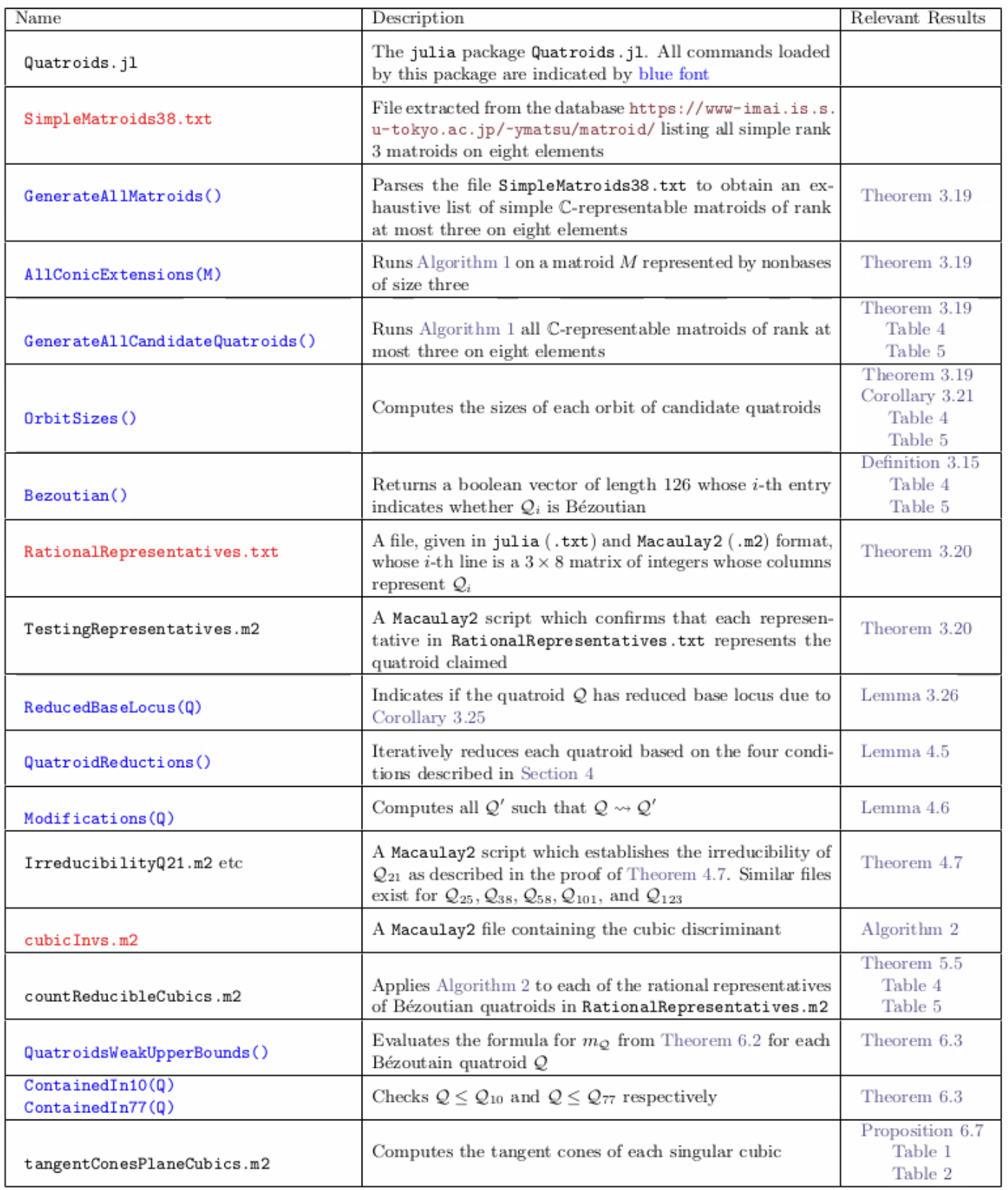
Descriptions of the Auxiliary Files
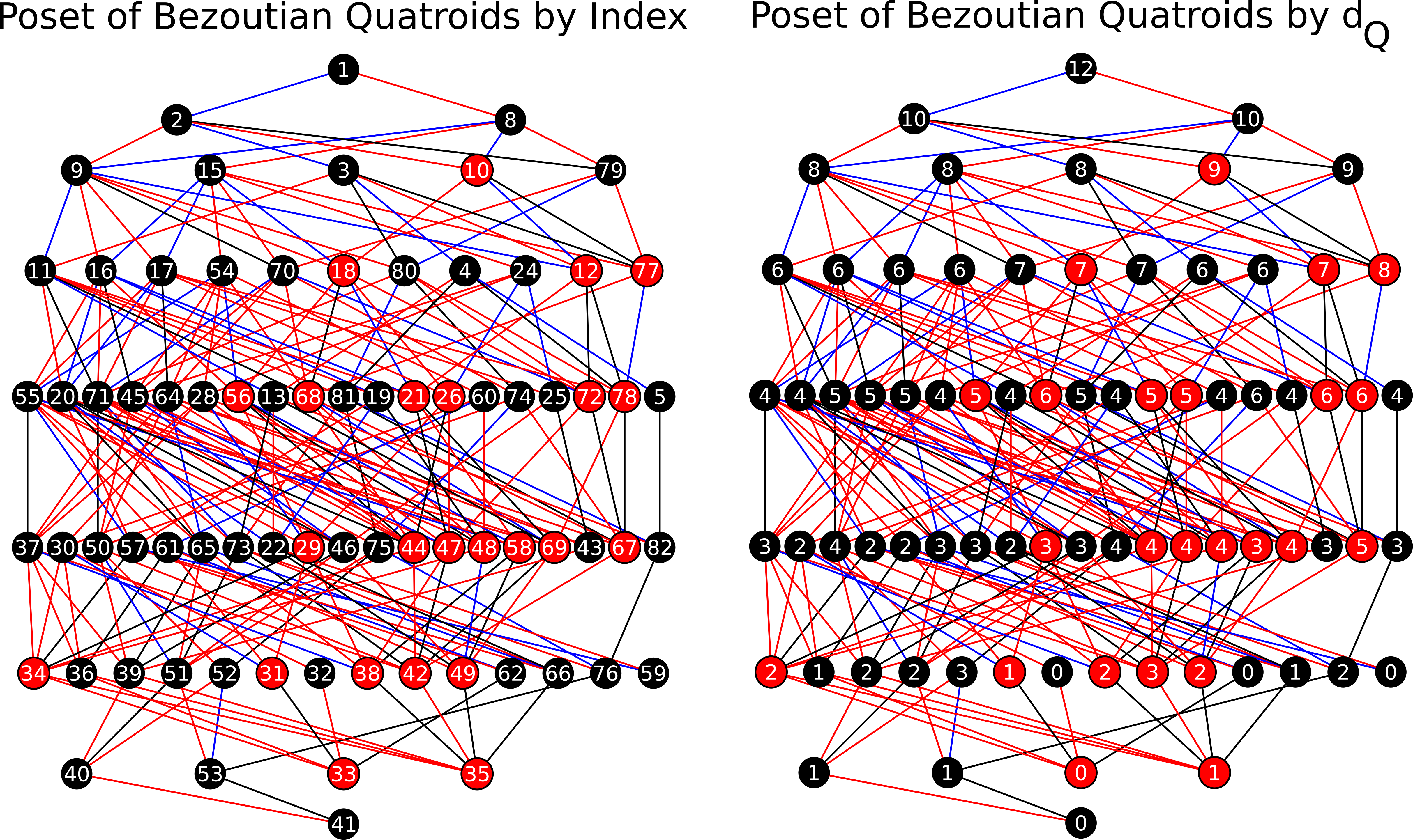
The Poset of Orbits of Bezoutian Quatroids
The following image can also be downloaded here:
Poset.png
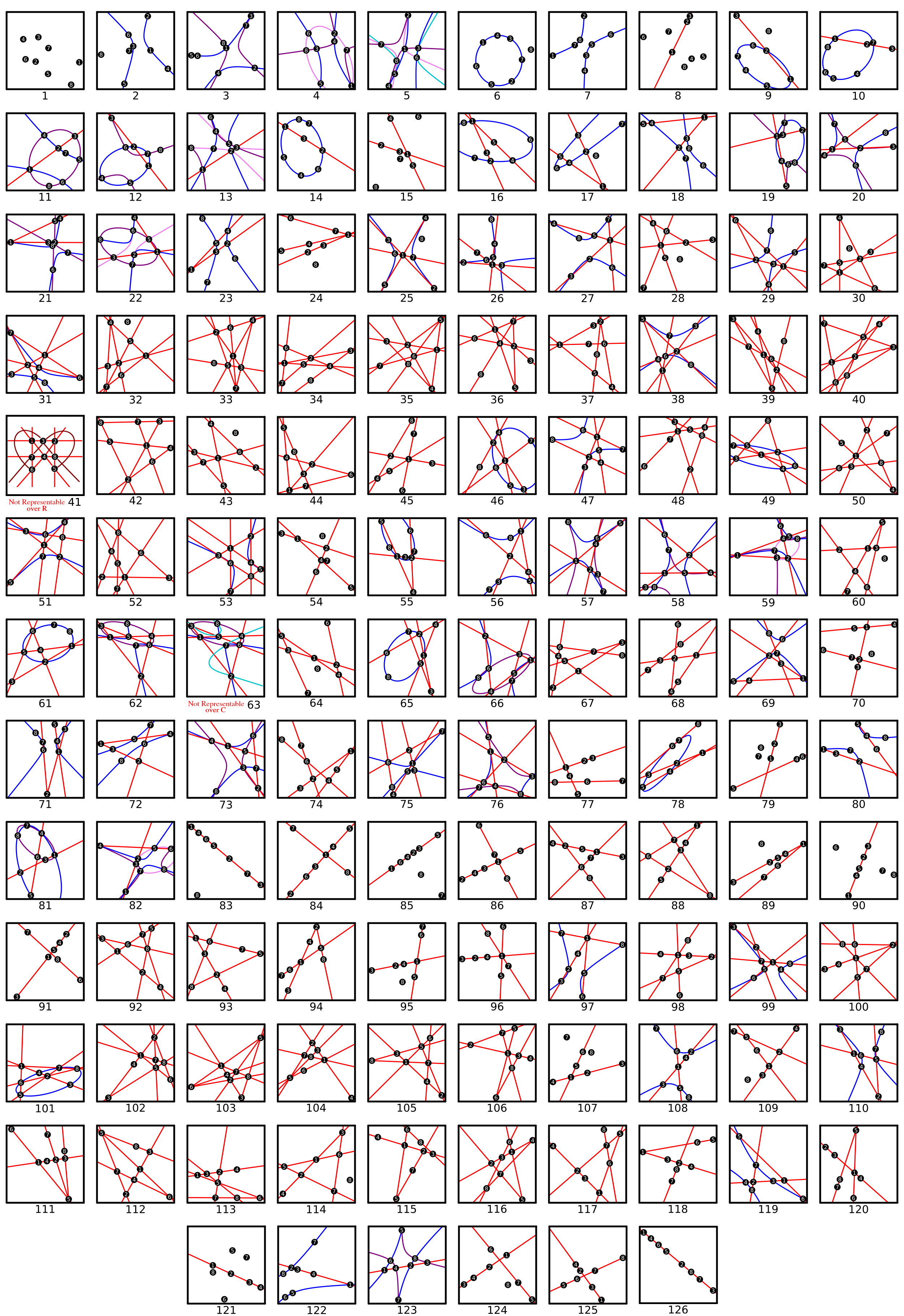
Illustrations of Candidate Quatroids
The following image can also be downloaded here:
QuatroidsImage.png
Project page created: 4/9/2023
Project contributors: Taylor Brysiewicz, Fulvio Gesmundo, Avi Steiner
Corresponding author of this page: Avi Steiner, avi.steiner@gmail.com
Macaulay2 code written by: Fulvio Gesmundo
Julia code written by: Taylor Brysiewicz
Jupyter notebooks written by: Avi Steiner
Software used: Julia (Version 1.9.3), Macaulay2 (v1.22)
System setup used: MacBook Pro with macOS 13.5.1 with Apple M2 Pro, 16 GB RAM
License for code of this project page: MIT License (https://spdx.org/licenses/MIT.html)
License for all other content of this project page (text, images, …): CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/)
Last updated 14/9/2023.