Santaló Geometry of Convex Polytopes

This page contains auxiliary files to the paper:
Dmitrii Pavlov, and Simon Telen: Santaló Geometry of Convex Polytopes
ARXIV: https://arxiv.org/abs/2402.18955
ABSTRACT: The Santaló point of a convex polytope is the interior point which leads to a polar dual of minimal volume. This minimization problem is relevant in interior point methods for convex optimization, where the logarithm of the dual volume is known as the universal barrier function. When translating the facet hyperplanes, the Santaló point traces out a semi-algebraic set. We describe and compute this geometry using algebraic and numerical techniques. We exploit connections with statistics, optimization and physics.

We implemented algorithms for computing Santaló points and Santaló patchworks in Julia using the Oscar computer algebra package and HomotopyContinuation numerical algebraic geometry package. Our code can be downloaded here: Santalo.zip. Instructions on how to run it are contained in the comments in source code files. The file Santalo.jl containing our package should be located in the folder named Santalo inside the directory of your project. To use it, in the Julia package manager you should run activate Santalo and instantiate().

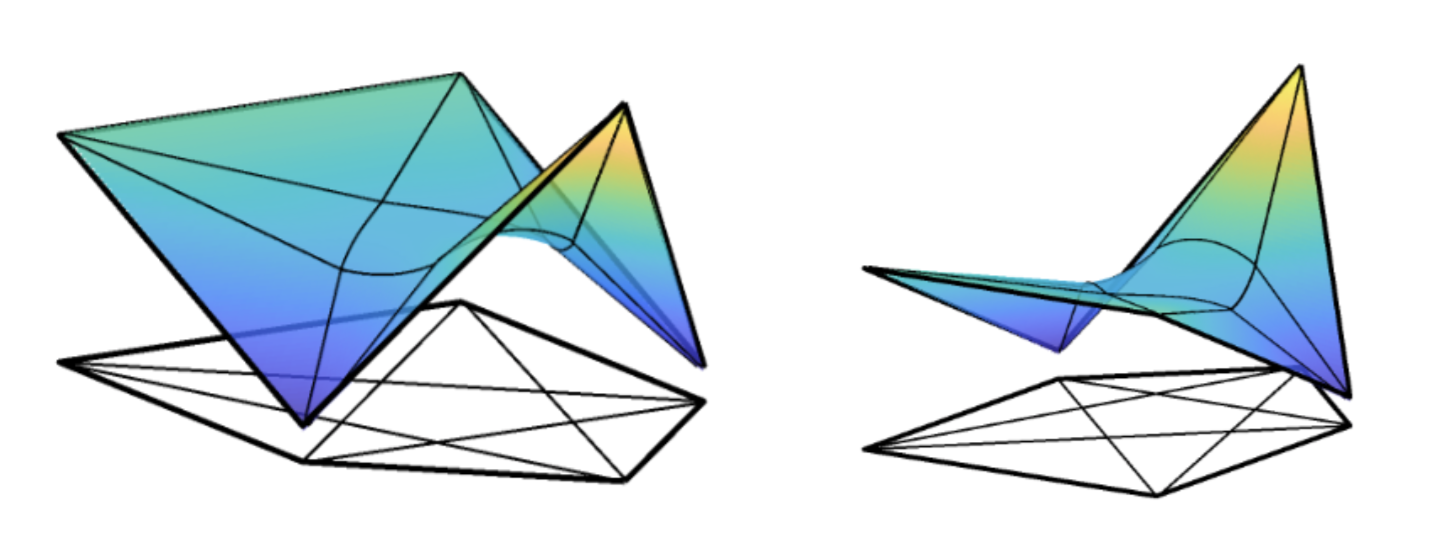
The figure below illustrates a projection to the three-dimensional space of the Santaló patchwork of the matrix

\[\begin{split}A \, = \, \begin{bmatrix} 1 & 1 & 1 & 1 & 1\\ 2 & 1 & 0 & 1 & 0\\ 1 & 2 & 0 & 0 & 1 \end{bmatrix}.\end{split}\]
../_images/patch_proj.png

Project page created: 28/02/2024.

Project contributors: Dmitrii Pavlov, Simon Telen.

Corresponding author of this page: Dmitrii Pavlov, pavlov@mis.mpg.de.

Software used: Julia (Version 1.9.1), Oscar (Version 0.14.0), HomotopyContinuation.jl (Version 2.9.3).

System setup used: MacBook Pro with macOS Monterey 12.6, Processor 2,8 GHz Intel Core i7, Memory 16 GB 2133 MHz LPDDR3, Graphics Intel HD Graphics 630 1536 MB.

License for code of this project page: MIT License (https://spdx.org/licenses/MIT.html).

License for all other content of this project page (text, images, …): CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).

Last updated 01/03/24.