Tangent Quadrics in Real 3-Space
In this article, we derive the polynomial conditions for quadrics in 3-space to contain a collection of points and to be tangent to a collection of lines and planes. When the number of such figures equals nine, there exist a finite number of quadrics which satisfy those conditions. The number of such quadrics is given by the corresponding entry in Schubert’s triangle.
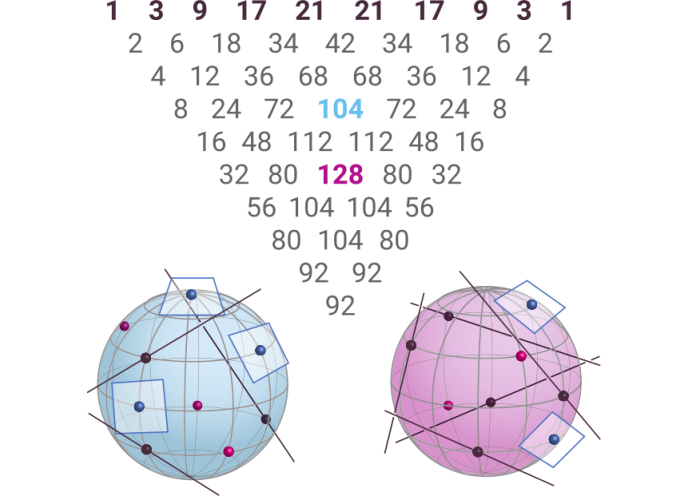
Our article serves as a first step towards showing that they can all be real. The following Jupyter notebook computes the number 104 (above in blue). The code is presented as a Jupyter notebook in julia and the main computations rely on the package HomotopyContinuation.jl.
The functions which construct the polynomial systems, verify the nondegeneracy of solutions, and reproduce the certification computations may
be downloaded here TangentQuadricsCode.zip. Simply unzip the folder and open TangentQuadrics.ipynb in a Jupyter notebook.
The certification files may be downloaded here Certificates.zip.
In Lemma 2.1 we prove that the condition in the projective space for two quadrics to be tangent corresponds to the vanishing of the discriminant of the determinant of a linear combination of the two quadrics. This is an irreducible polynomial and the Maple code we used to compute it can be viewed here:
Project page created: 21/10/2020
Code contributors: Taylor Brysiewicz, Claudia Fevola, and Bernd Sturmfels
Jupyter Notebook written by: Taylor Brysiewicz, 21/10/2020
Project contributors: Taylor Brysiewicz, Claudia Fevola, and Bernd Sturmfels
Software used: Julia
Corresponding author of this page: Taylor Brysiewicz, Taylor.Brysiewicz@mis.mpg.de