Tropical Implicitization

Here you may find the supplementary codes for the paper:
Kemal Rose, Bernd Sturmfels, Simon Telen: Tropical implicitization revisited
ARXIV: https://arxiv.org/abs/2306.13015 CODE: https://mathrepo.mis.mpg.de/TropicalImplicitization

ABSTRACT: Tropical implicitization means computing the tropicalization of a unirational variety from its parametrization. In the case of a hypersurface, this amounts to finding the Newton polytope of the implicit equation, without computing its coefficients. We present a new implementation of this procedure in OSCAR.jl . It solves challenging instances, and can be used for classical implicitization as well. We also develop implicitization in higher codimension via Chow forms, and we pose several open questions.

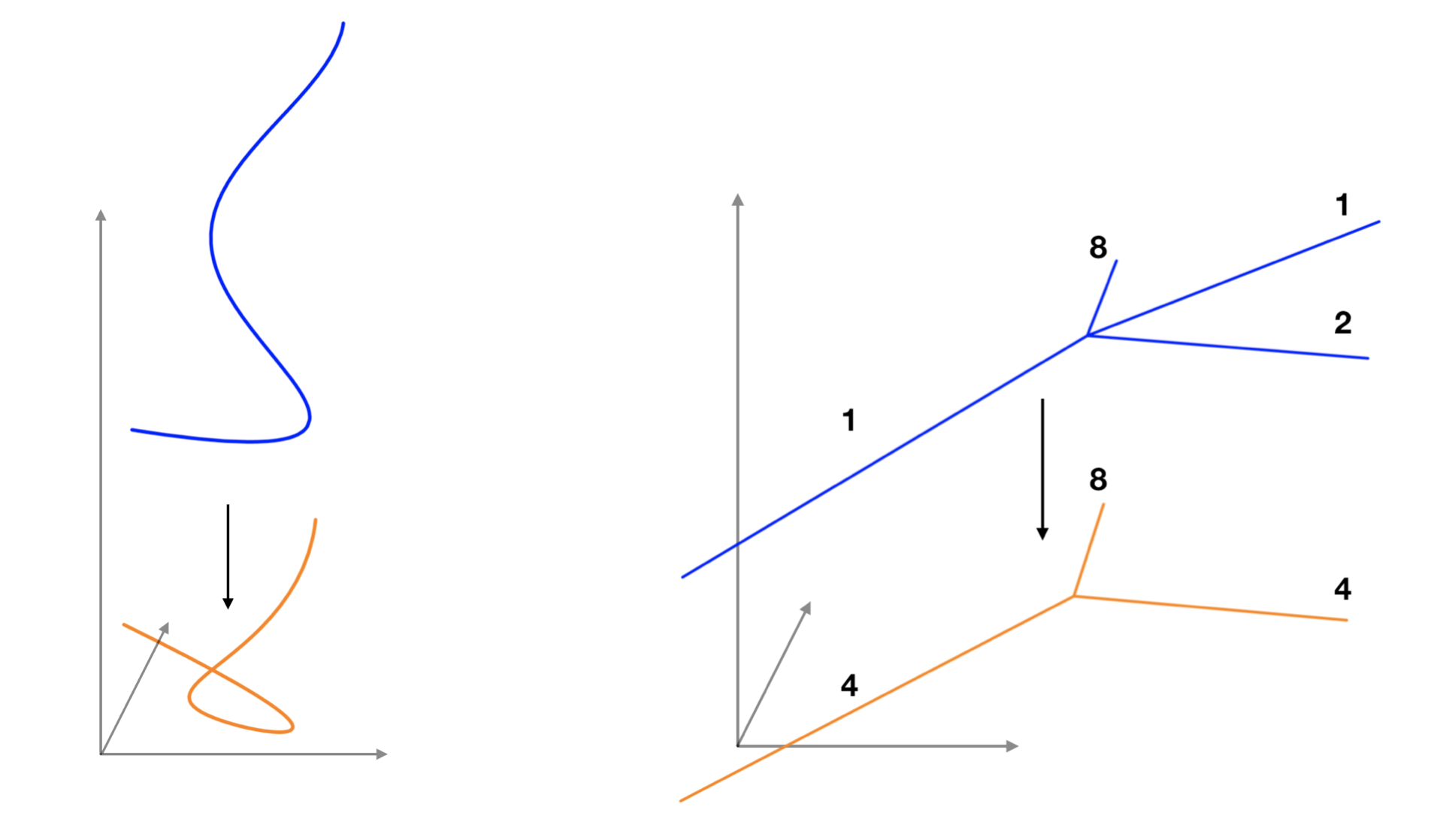
../_images/classVStrop.png

Example

Consider the parametrization \(:f = (f_1, f_2): \ \mathbb{C}^* \longrightarrow ( \mathbb{C}^*)^2\) given by

\[f_1 = 11 \, t^2 + 5 \, t^3 - t^4 \quad \text{and} \quad f_2 = 11 + 11 \, t + 7 \, t^8.\]

The image is the plane curve \(:C = \overline{\operatorname{im}f}\) given by the implicit equation \(:F(x,y) = 0\), with

\[F \, = \, 2401 \, x^8 - 1372 \,x^6y - 422576\,x^5y + \cdots + y^4 + \cdots + 1247565503668.\]

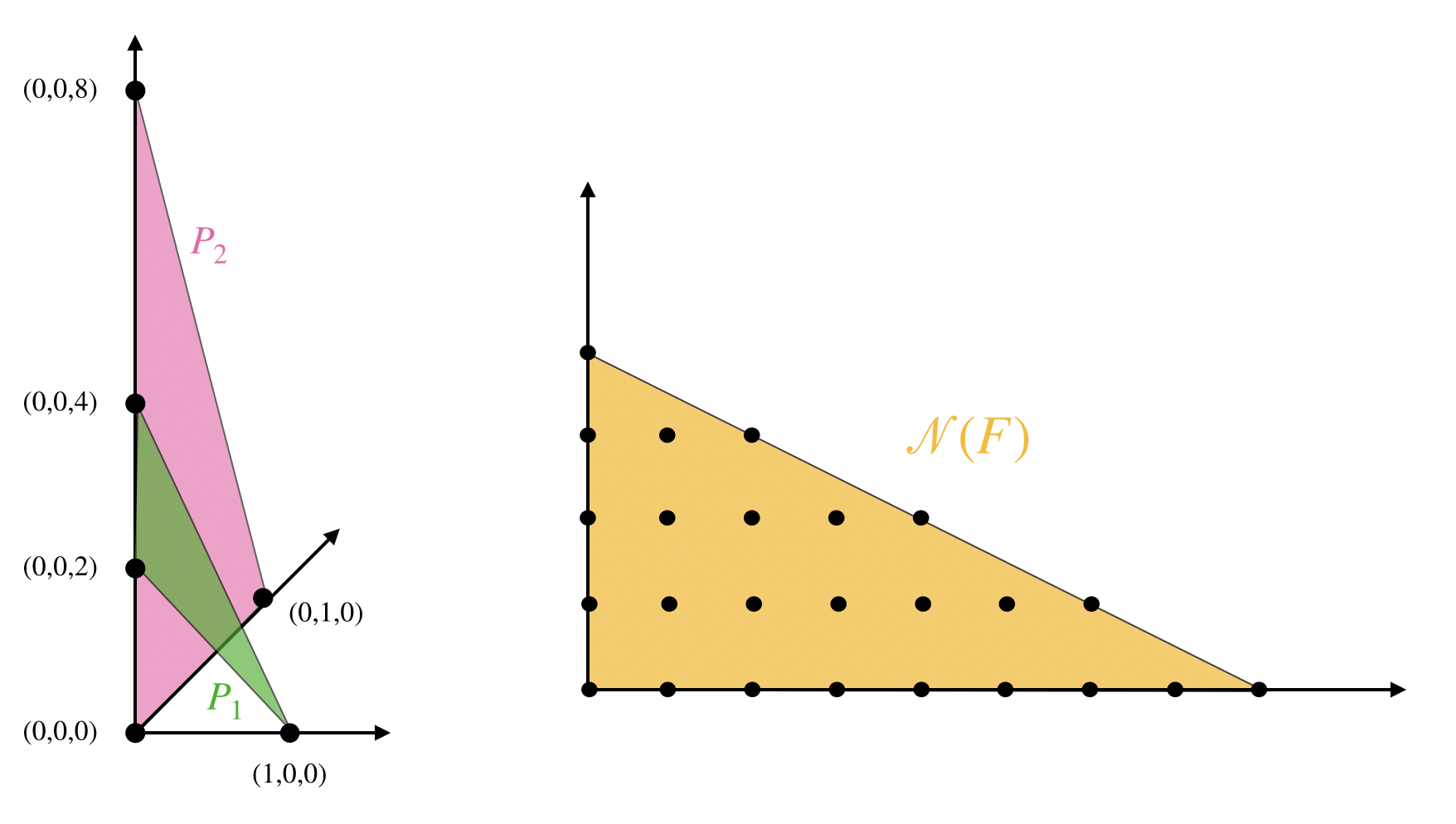
This has \(25\) terms, one for each lattice point of the Newton polytope \({\cal N}(F)\), shown on the right side of the Figure below. The Newton polytopes of \(:x-f_1\) and \(:y - f_2\) are the triangles seen on the left side.

../_images/polytopes.png

The following OSCAR.jl code computes \(:{\cal N}(F)\):

using tropicalimplicitization, Oscar
R, (t,) = polynomial_ring(QQ,["t"])
f1 = 11* t^2 + 5*t^3 - 1*t^4
f2 = 11 + 11*t + 7*t^8
Q1 = newton_polytope(f1)
Q2 = newton_polytope(f2)
newton_pols = [Q1, Q2]
cone_list, weight_list = get_tropical_cycle(newton_pols)
Delta = get_polytope_from_cycle(cone_list, weight_list)

A-discriminants

The hyperdeterminant of multidimensional tensor vanishes whenever the hypersurface defined by the associated multilinear form is singular. In the notation of section 3, this is the \(A\)-discriminant \(\Delta_A\), where the columns of \(A\) are the vertices of a product of simplices. As an illustration, we here present the hyperdeterminant of format \(2 \times 2 \times 2\). Here the columns of \(A\) are the vertices of the regular \(3\)-cube:

\[\begin{split}A \, = \,\begin{bmatrix} \,1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \, \\ \,0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \,\\ \,0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \,\\ \,0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \, \\ \end{bmatrix}\end{split}\]

The hyperdeterminant has the form

\[\begin{split}\begin{matrix} \Delta_A \,\,=\,\, x_{000}^2x_{111}^2 +x_{001}^2 x_{110}^2 +x_{011}^2 x_{100}^2 +x_{010}^2 x_{101}^2 + 4 x_{000} x_{011} x_{101} x_{110} +4 x_{001} x_{010} x_{100} x_{111} & \\ -\,2 x_{000} x_{001} x_{110} x_{111} -2 x_{000} x_{010} x_{101} x_{111} -2 x_{000} x_{011} x_{100} x_{111} & \\ -\,2 x_{001} x_{010} x_{101} x_{110} -2 x_{001} x_{011} x_{100} x_{110} -2 x_{010} x_{011} x_{100} x_{101}. & \end{matrix}\end{split}\]

It is computed with the following code:

A = [1 1 1 1 1 1 1 1; 0 0 0 0 1 1 1 1; 0 0 1 1 0 0 1 1; 0 1 0 1 0 1 0 1]
cone_list, weight_list = get_trop_A_disc(A)
Delta = get_polytope_from_cycle(cone_list, weight_list)

Code

The source code can be downloaded here:TropicalImplicitization.jl.

Project page created: 21/06/2023

Project contributors: Kemal Rose, Simon Telen and Bernd Sturmfels.

Software used: Julia(Version1.8), Oscar(Version0.12.0)

Corresponding author of this page: Kemal Rose, krose@mis.mpg.de.