Twisted Cohomology and Likelihood Ideals
ABSTRACT: A likelihood function on a smooth very affine variety gives rise to a twisted de Rham complex. We show how its top cohomology vector space degenerates to the coordinate ring of the critical points defined by the likelihood ideal. We obtain a basis for cohomology from a basis of this coordinate ring. We investigate the dual picture, where twisted cycles correspond to critical points. We show how to expand a twisted cocycle in terms of a basis, and apply our methods to Feynman integrals from physics.
The following picture illustrates Lefschetz thimbles, which constitute a natural basis for twisted homology on the one dimensional torus with the third roots of unity removed.
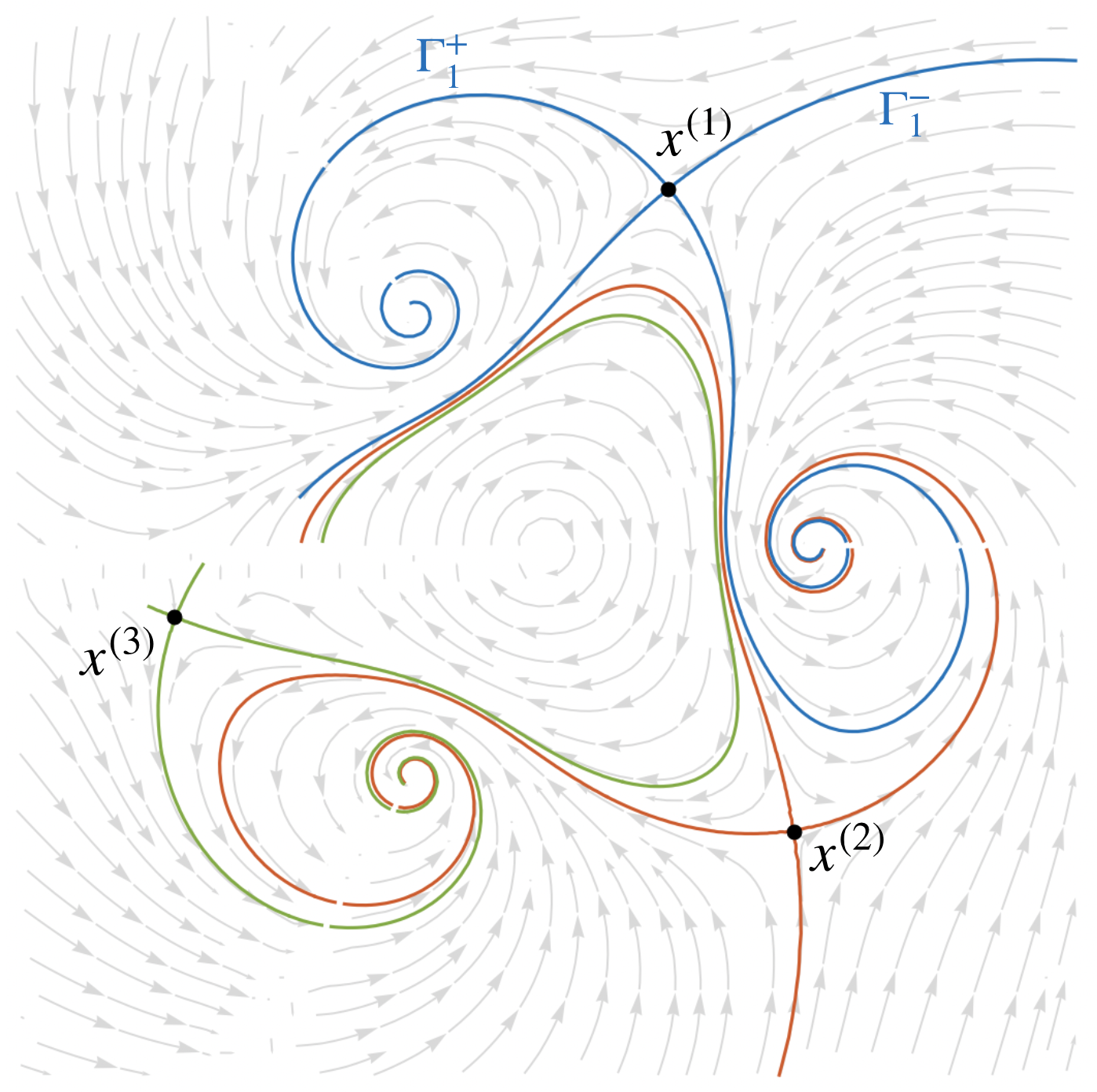
This picture was generated using Mathematica. The script can be downloaded here: lefschetz.zip.
We implemented our algorithms in julia (v1.8.3) using the packages HomotopyContinuation.jl (v2.6.4) and Oscar.jl (v0.10.0). We include our implementation in this repository.
To download the code, click here code.zip. The results of the computations reported in Section 6 can be found in txt format here results_Sec6.zip.
Project page created: 31/01/2023
Project contributors: Saiei-Jaeyeong Matsubara-Heo and Simon Telen
Corresponding author of this page: Simon Telen, Simon.Telen@mis.mpg.de
Software used: Julia (Version 1.8.3), Mathematica (Version 12.3.1)