The algebraic degree of the Wasserstein distance
Abstract. Given two rational univariate polynomials, the Wasserstein distance of their associated measures is an algebraic number. We determine the algebraic degree of the squared Wasserstein distance, serving as a measure of algebraic complexity of the corresponding optimization problem. The computation relies on the structure of a subpolytope of the Birkhoff polytope, invariant under a transformation induced by complex conjugation.
Overview
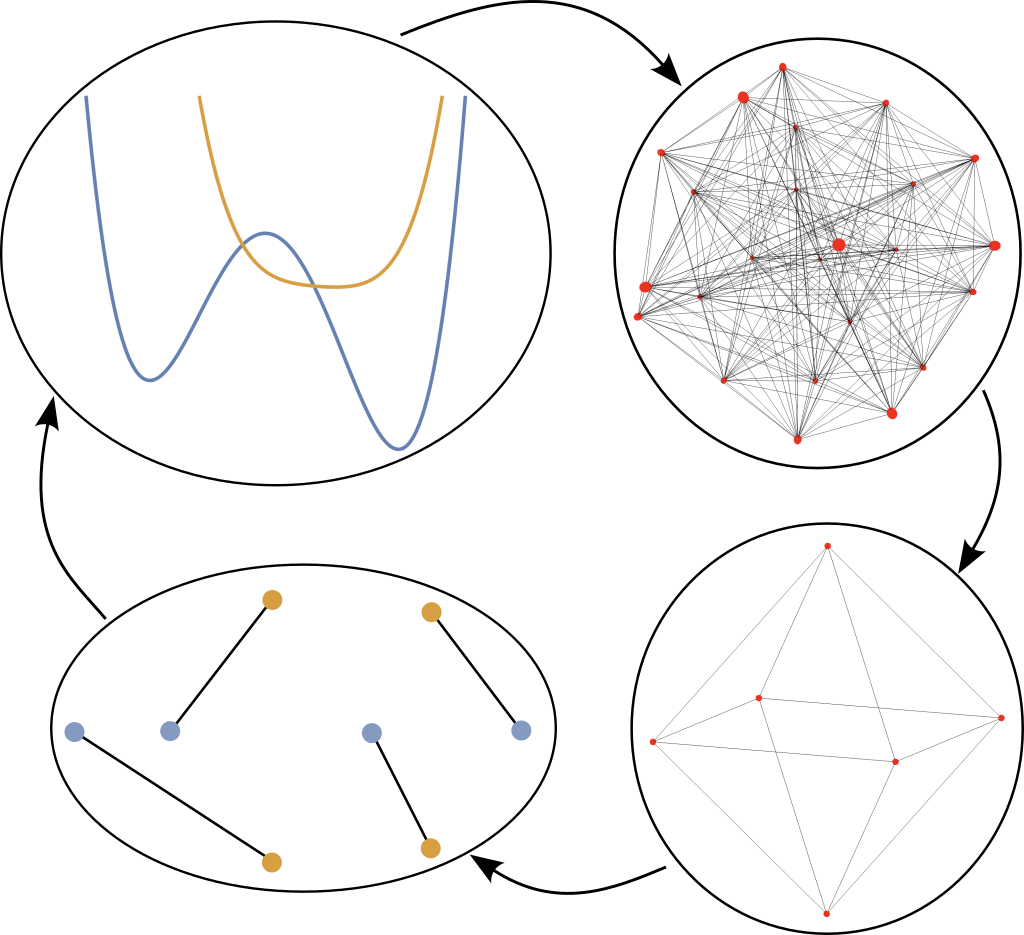
The picture illustrates the process of computing the Wasserstein distance: On the top-left, we start with two rational polynomials of degree 4. The Wasserstein distance can be computed is a linear program on the Birkhoff polytope of doubly stochastic matrices of size 4, shown on the top right. As we consider two real polynomials, we can actually compute the Wasserstein distance as a linear program on a subpolytope, that we call the invariant Birkhoff polytope, here shown on the lower right. The lower left then shows an optimal assignment.
The following Jupyter notebooks provide code using the julia packages OSCAR and HomotopyContinuation.jl.
They can be downloaded here: julia_code.zip
Project page created: 25/06/2024
Project contributors: Chiara Meroni, Bernhard Reinke, and Kexin Wang
Corresponding author of this page: Bernhard Reinke, bernhard.reinke@mis.mpg.de
Software used: Julia (Version 1.10.2)
System setup used: Asus ZenBook UX305F, CPU: 900MHz Intel Core M3-6Y30 (dual-core, 4MB cache, 2.2GHz with Turbo Boost) RAM: 8GB DDR3L
License for code of this project page: MIT License (https://spdx.org/licenses/MIT.html)
License for all other content of this project page (text, images, …): CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/)
Last updated 25/06/2024.