Plane Sextic Curves

What are the the possible topological types of a smooth real algebraic curve of a certain degree in projective plane? For degree less than six the answer is straight forward by Bézout Theorem. The classification of curves of degree six is included in Hilbert’s famous collection of problems in 1900. This is part of Hilbert’s 16th problem. Many mathematicians worked on this problem but only in 1969 the answer was completed by Gudkov. He could find the last two missing constructions and proved that there are exactly 56 different topological types for plane sextic curves.

To see more about the computational studies on these curves please check:

Nidhi Kaihnsa, Mario Kummer, Daniel Plaumann, Mahsa Sayyary Namin, and Bernd Sturmfels: Sixty-four curves of degree six

In: Experimental mathematics, 28 (2019) 2, p. 132-150

MIS-Preprint: 23/2017 DOI: 10.1080/10586458.2017.1360808 ARXIV: https://arxiv.org/abs/1703.01660 CODE: https://mathrepo.mis.mpg.de/planeSexticCurves

for which we wrote a software in mathematica to determine the topological type of a plane sextic. There is a finer classification than topological type, which is called rigid isotopy classification. We have also made a list of 64 examples for each 64 rigid isotopy type of plane sextics. Both can be found here:

• Sextic Classifier
• Sextic Curves

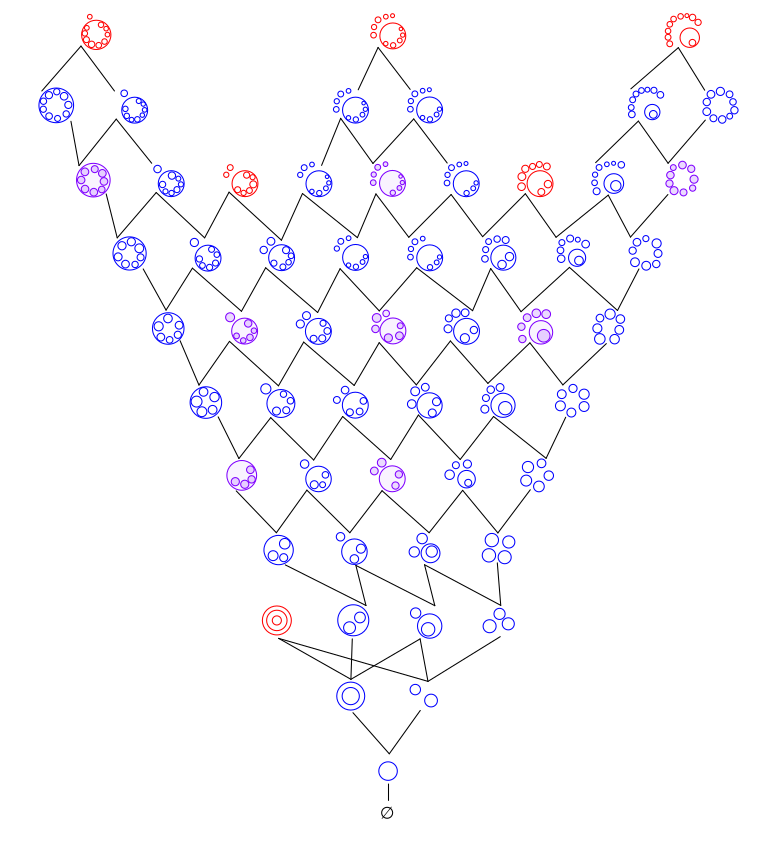
Here you see 56 topological types and 64 rigid isotopy types of plane sextics. The colors red and blue are used to show curves of dividing types and non-dividing types, respectively. There are 8 topological types that can be either dividing or non-dividing. They are colored in purple. If you are interested to see the poset structure of these types you can find more explanation in the publication cited above.

Project contributors: Nidhi Kaihnsa, Mario Kummer, Daniel Plaumann, Mahsa Sayyary Namin, and Bernd Sturmfels

Software used: Mathematica