An SOS counterexample to an inequality of symmetric functions

This page contains auxiliary files to the paper:

Alexander Heaton and Isabelle Shankar: An SOS counterexample to an inequality of symmetric functions

In: Journal of pure and applied algebra, 225 (2021) 8, 106656

MIS-Preprint: 86/2019 DOI: 10.1016/j.jpaa.2020.106656 ARXIV: https://arxiv.org/abs/1909.00081 CODE: https://mathrepo.mis.mpg.de/soscounterexample

In this article, we demonstrate a counterexample to a conjecture relating nonnegativity of certain symmetric functions with the dominance/majorization partial order on partitions. The code is presented as a Jupyter notebook in SageMath 9.2. This Jupyter notebook computes an exact, rational, sum of squares certificate of nonnegativity for a certain symmetric polynomial. This polynomial is formed as the difference of two homogeneous symmetric polynomials corresponding to a pair of partitions which are incomparable in dominance order. More details are explained in the accompanying paper, and also in the Jupyter notebook.

• An SOS counterexample to an inequality of symmetric functions

The matrices required for the computation are saved as .sobj files, which can be downloaded here counterexample-A and counterexample-P. The Jupyter notebook can be downloaded here: verifysoscertificate.ipynb.

Alternatively, you can run the computations yourself using CoCalc and its public server. Follow this link, and then click “Open with one click”. You should be able to execute the code yourself, verifying the counterexample. This can also be done by downloading the files above and running them locally on your own machine.

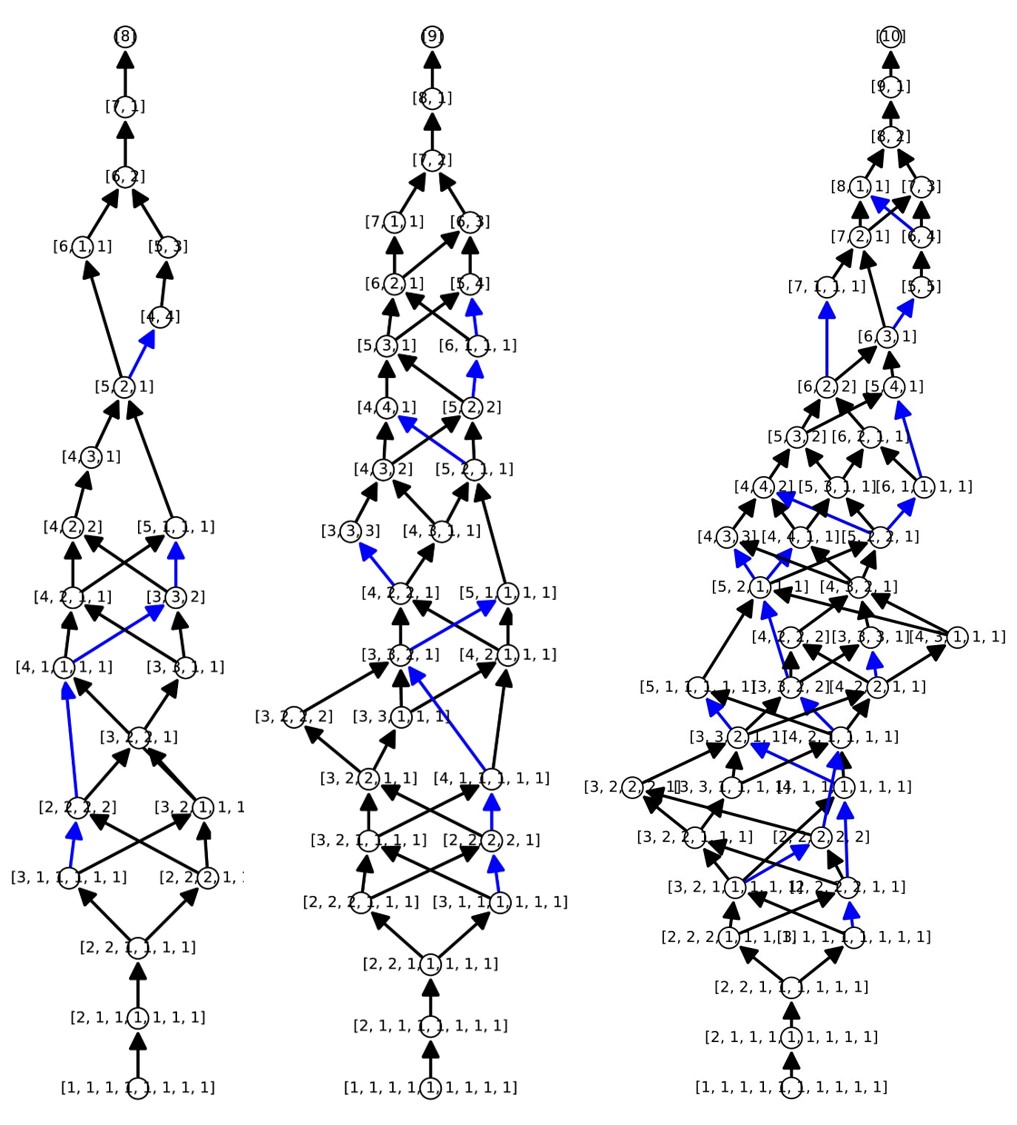
Below is an image showing the dominance order on partitions of 8, 9, and 10 corresponding to the black arrows. Every blue arrow is a relationship of nonnegativity, as verified by numerical SOS decompositions found using the symmetry-adapted techniques of our paper. Every blue arrow is a counterexample to the conjecture. The code in the Jupyter notebook above gives a provably correct counterexample, since for that blue arrow, we took the time to find an exact, rational SOS decomposition, which of course requires much more effort.

Project page created: 04/11/2020

Code contributors: Alexander Heaton and Isabelle Shankar

Project contributors: Alexander Heaton and Isabelle Shankar

Jupyter Notebook written by: Alexander Heaton, 03/11/2020

Software used: SageMath 9.2

Corresponding author of this page: Alexander Heaton, alexheaton2@gmail.com