Type (020)
A tropical curve of type (020) is of the form
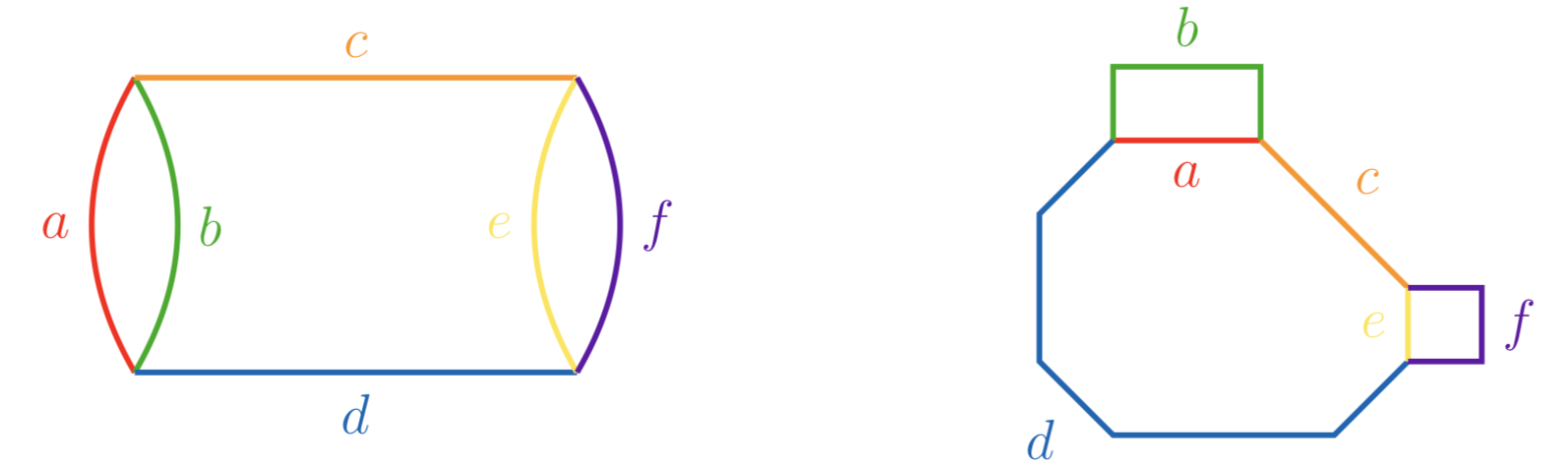
Due to symmetry, we may assume that \(a\leq b\), \(c\leq d\) and \(e\leq f\), as well as \(b-a\leq f-e\). It can be realized as a plane tropical curve if and only if \(c + a \leq d\) and \(c + e \leq d\), and if one of two inequalities is an equality, and \(a=b\), then \(a<e<f\).
To illustrate how a curve is embeddable as a tropical quartic curve in a tropical plane, consider the following configuration of lengths which does not satisfy any of the previous three inequalities:
Consider the degenerate tropical curve given by the quartic polynomial
poly g = (1-2t9+3t20+t2+t7)+(2-3t9+4t20+t2)*x+x^2+(1-t6)*xy+x2y+t4x2y2+t6x3y+t9x3+t20x4+t4y+t9y2+t6xy2+t13xy3+t19y3+t30y4;
drawTropicalCurve(g,"max");

It is has edge lengths
and the modification \(z=x-1\), which goes along \(w_x=0\), yields the following tropical curve after projecting onto the \(zy\) plane (\(y\) remaining the vertical direction):
poly g1 = subst(g,x,x-1);
drawTropicalCurve(g1,"max");

The entirety of \(w_x<0\) is mapped onto \(w_z=0\), while the edge on the line \(w_x=0\) has been enlarged to length \(10\).