Type (111)
Plane quartics of type (111)
A tropical curve of type (111) is of the form
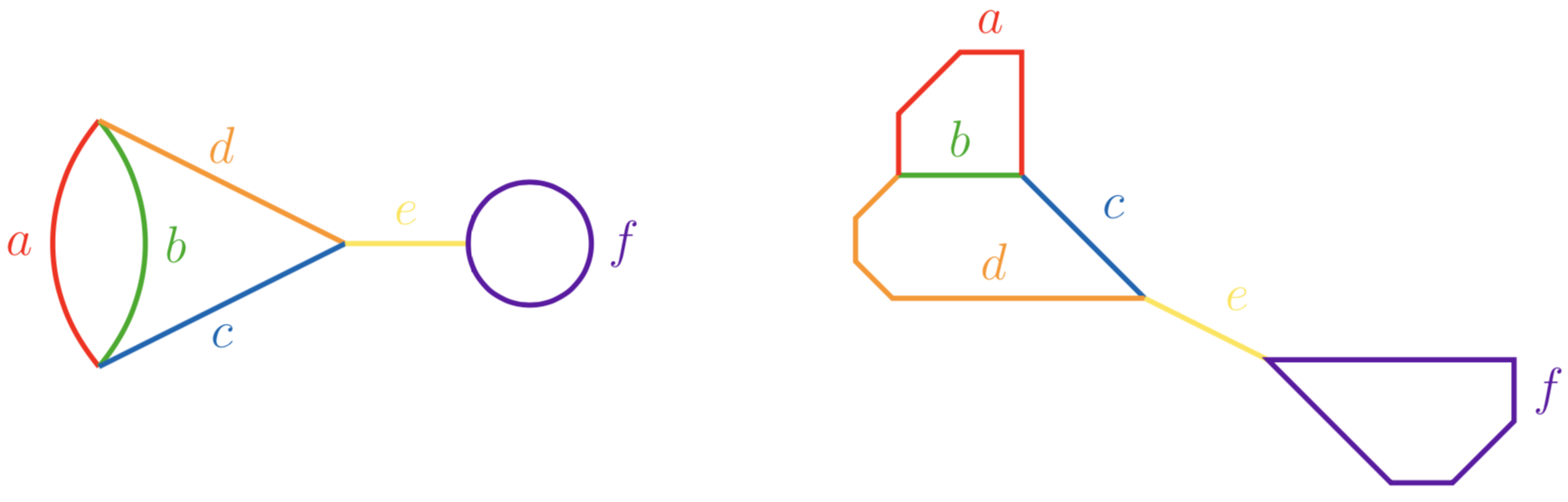
By symmetry, we may assume that \(a\leq b\) or \(b\leq a\) and \(c\leq d\) or \(c\geq d\). Due to the positioning of the edges in plane tropical curves of type (111), we choose \(b\leq a\) and \(c\leq d\). Moreover, as the curve is not realizably hyperelliptic, we may also assume \(c\neq d\).
These curves can be realized as tropical plane quartics if and only if \(b+c<d<b+3c\). Hence there are two classes of tropical quartics of type (111) which cannot be realized as tropical plane quartics:
curves with \(d\leq b+c\)
curves with \(d\geq b+3c\)
Quartics of type (111) with \(d\geq b+c\)
To realize curves with \(d\leq b+c\), say
we begin with a plane tropical quartic with correct lengths \(a,c,d,e,f\) and length \(b':=d-c\), whose edge of length \(b'\) we may unfold to an edge of length \(b\). For example, the tropical plane quartic
poly g = 2t2+t3x-y+t14x2-xy+y2+t27x3+t6x2y+xy2+t4y3+t44x4+t21x3y+t2x2y2+t5xy3+t10y4;
drawTropicalCurve(g,"max");
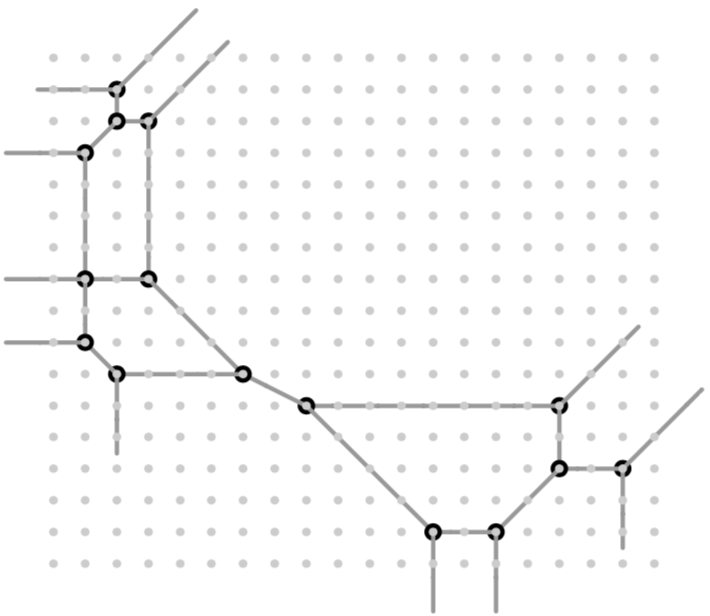
reveals the actual length of edge \(b\) to be 4 after the modification \(y=z+1\) (\(y\) remaining the vertical direction):
poly g1=substitute(g,y,y+1);
drawTropicalCurve(g1,"max");

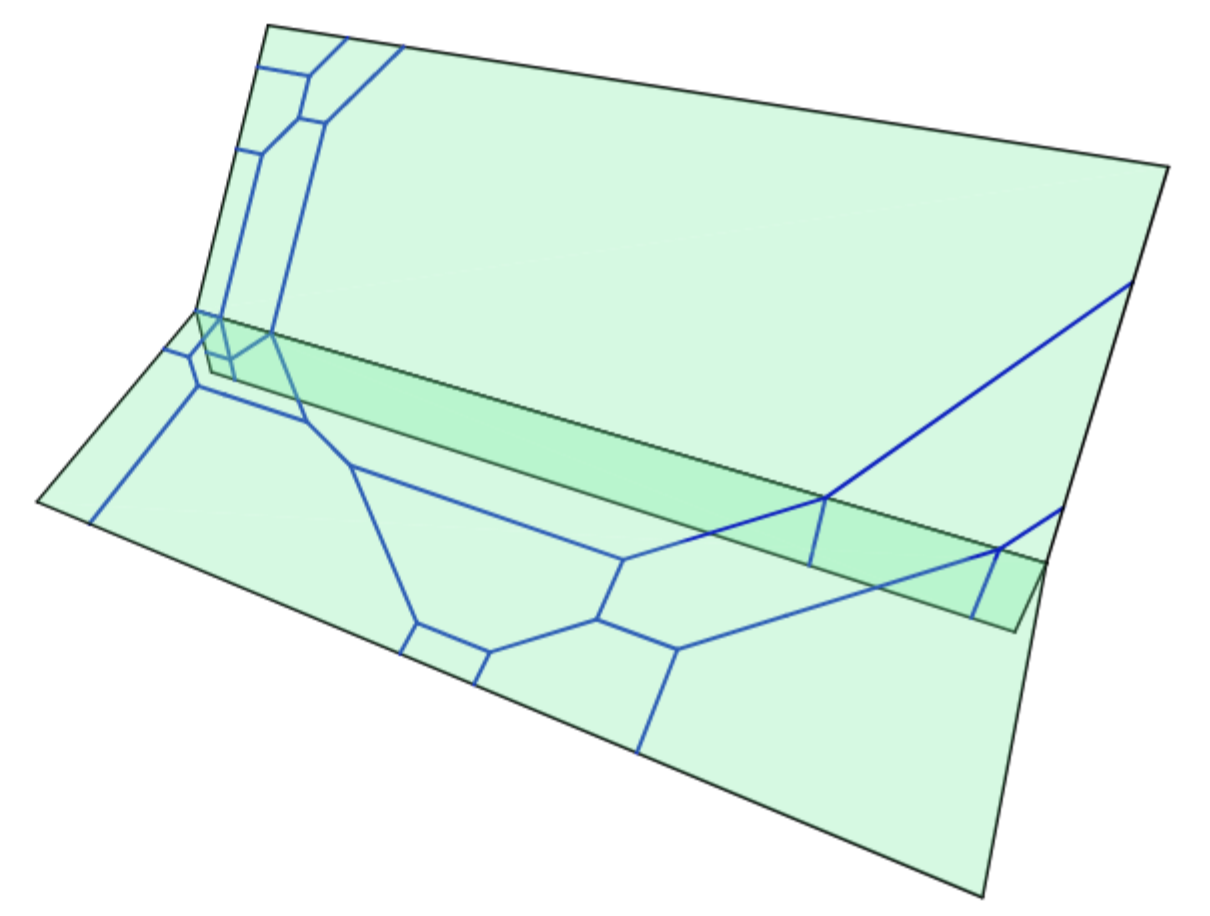
Thus, the tropicalization of \(\langle g,y-(z+1) \rangle\) yields a tropical quartic inside the tropical plane given by \(y-(z+1)\) with the desired skeleton:
Quartics of type (111) with \(d\geq b+3c\) and \(a<b\)
To realize curves with \(d>b+3c\) and \(a>b\), say
we begin with a plane tropical quartic with correct lengths \(a,b,c,d\) and edges with higher multiplicity which reveal a bounded edge of length \(e\) and cycle of length \(f\) after suitable modifications. For example the tropical plane quartic
poly g = t18+t6*x+(1-t4)*x2+t24*x4+t11*y+xy-2x2y+t8*y2+t3*xy2-x2y2+t12*y3+t8*xy3+t18*y4;
drawTropicalCurve(g,"max");
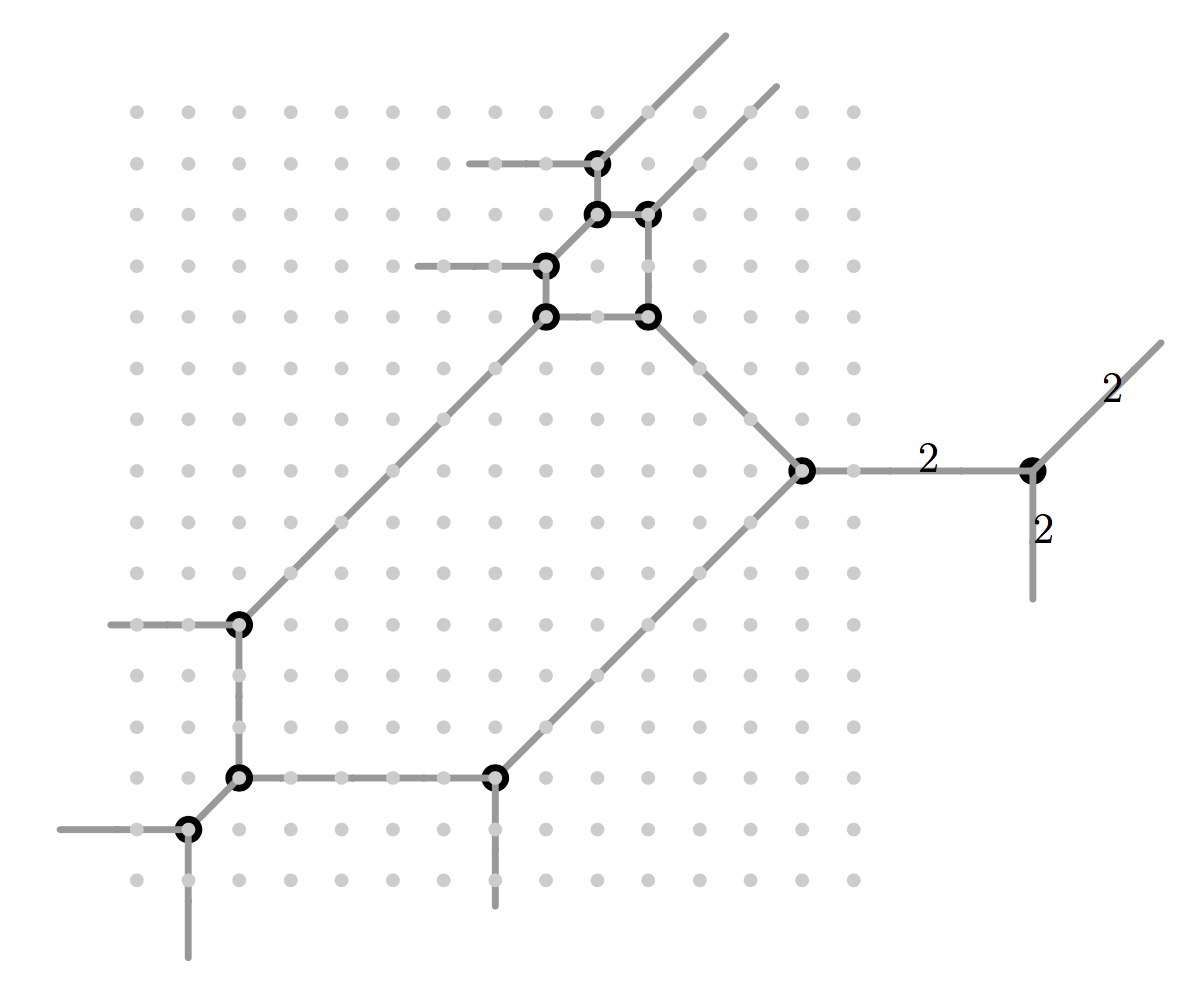
reveals an edge of length 2 and cycle of length 12 after the modification \(y=z+1+t^2\):
poly g1=substitute(g,y,y+1+t2);
drawTropicalCurve(g1,"max");

Therefore, the tropicalization of \(\langle g,y-(z+1+t^2) \rangle\) yields a tropical quartic inside the tropical plane given by \(y-(z+1+t^2)\) with the desired skeleton:
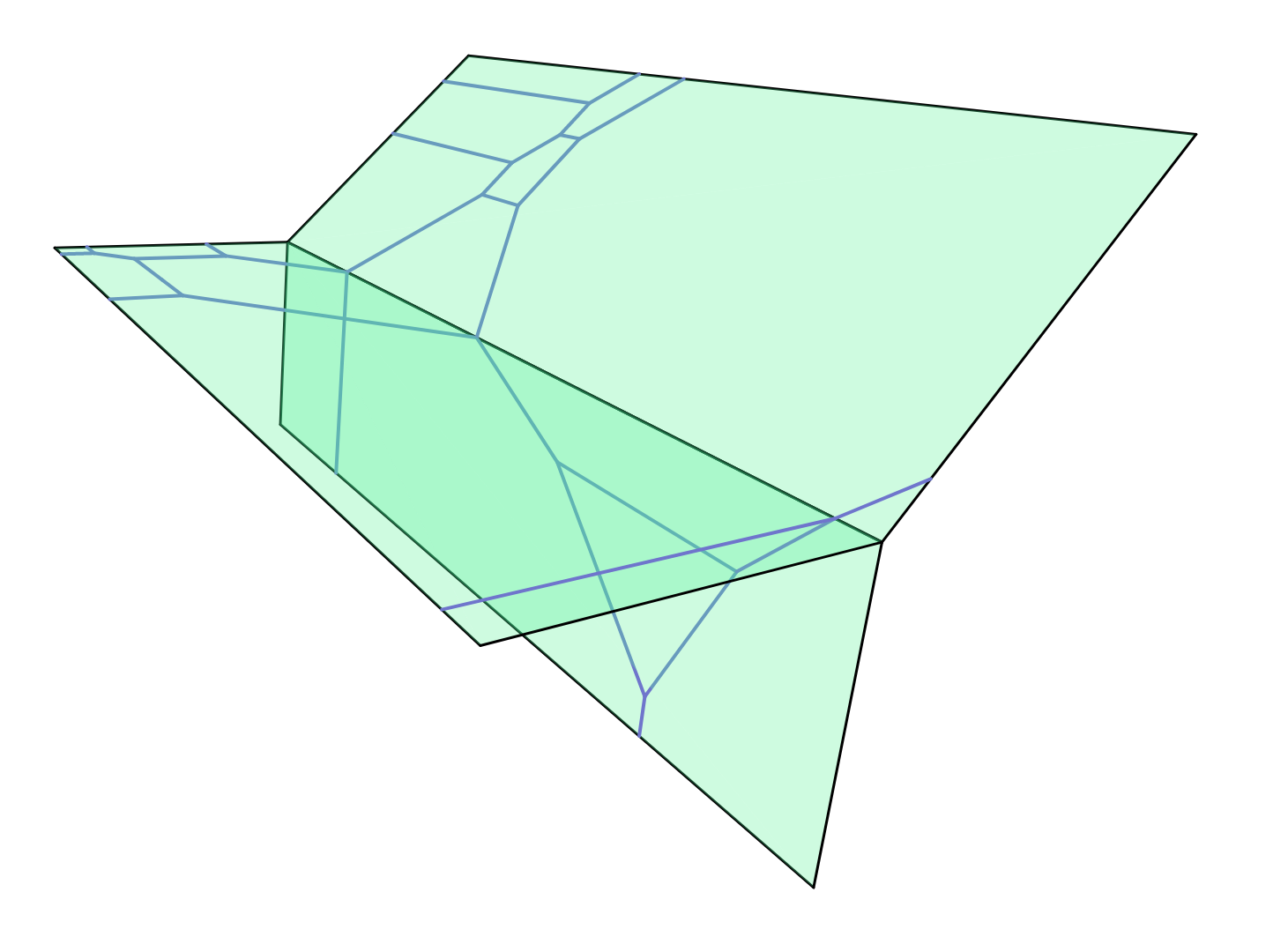
Quartics of type (111) with \(d\geq b+3c\) and \(a=b\)
To realize curves with \(d>b+3c\) and \(a=b\), say
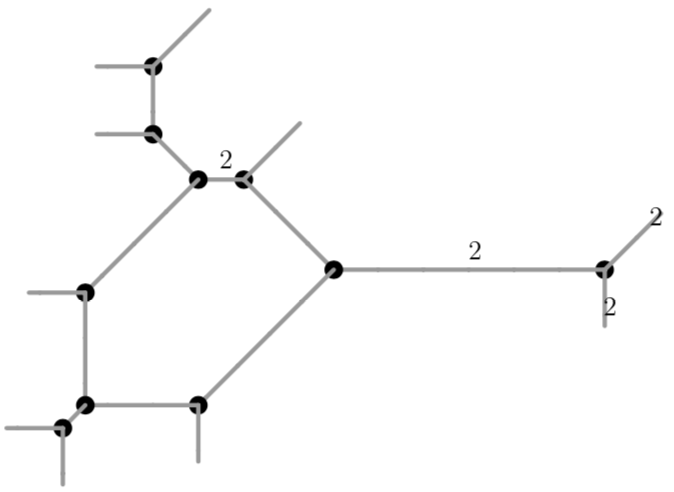
we begin with a more degenerate version of the plane starting curve in the case \(a>b\), in which edges \(a\) and \(b\) are collapsed into a single edge of length \(a=b\) of multiplicity two:
poly g = t18+t6*x+(1-t4)*x2+t24*x4+t11*y-xy-2x2y+t10*y2-x2y2+t16*y3+t8*xy3+t25*y4;
drawTropicalCurve(g,"max");
A modification then seperates the two edges of equal length:
poly g1=substitute(g,y,t^(-4)*y+t^(-4));
drawTropicalCurve(g1,"max");
