Type (212)
Plane quartics of type (212)
A tropical curve of type (212) is of the form
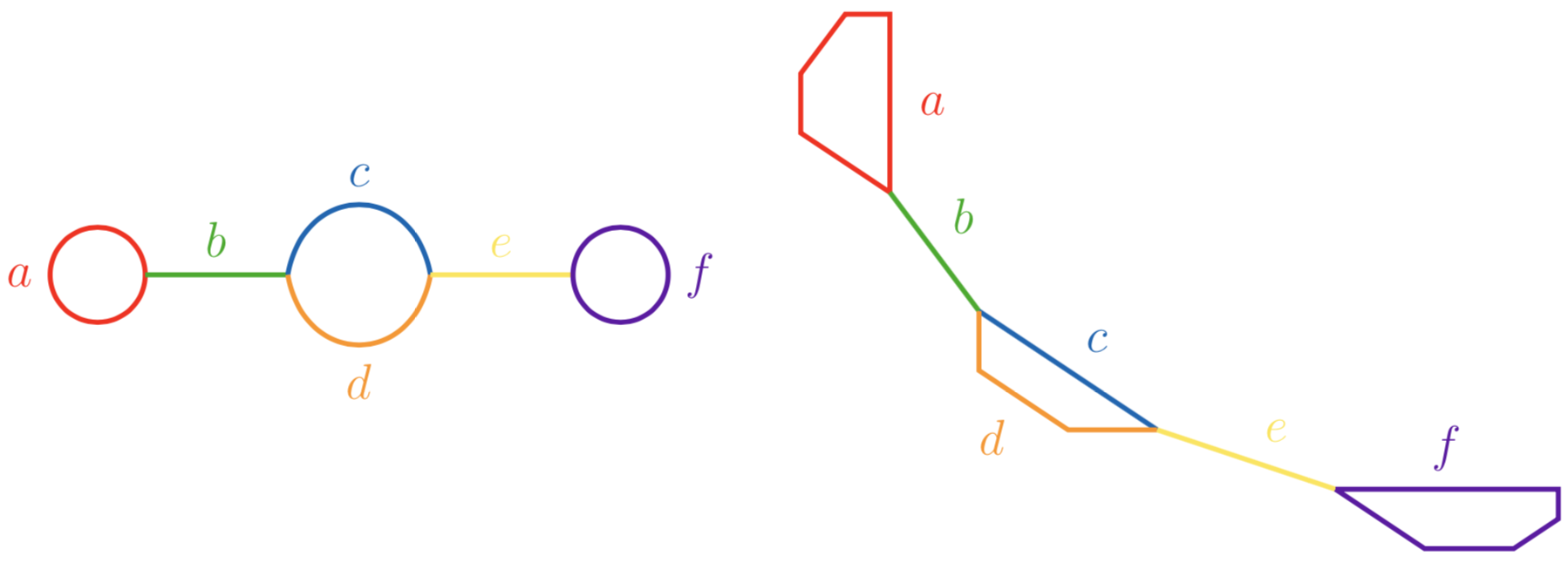
Due to symmetry, we assume \(d\geq c\). It is embeddable as a tropical quartic curve in \(\mathbb{R}^2\) if \(c<d\leq 2c\). However, curves with \(c=d\) are realizibly hyperelliptic, which is why we will ignore them in this context.
Quartics of type (212) with \(d>2c\)
To realize curves with \(d>2c\), we simply consider the degenerate tropical curve given by the quartic polynomial:
\[\begin{split}g&= t^{a+6b+2c}\cdot x^4 + t^{6e+f+2c}\cdot y^4 +x^2y^2+ 2\cdot xy^2 + (1-t^{2b}) y^2+ 2\cdot x^2y \\
& \quad +(1-t^{2e})\cdot x^2 + t^{-c} xy+ t^{\frac{-d+4c-1}{2}}y+ t^{\frac{-d+4c-1}{2}} x+ t^{-d+3c},\end{split}\]
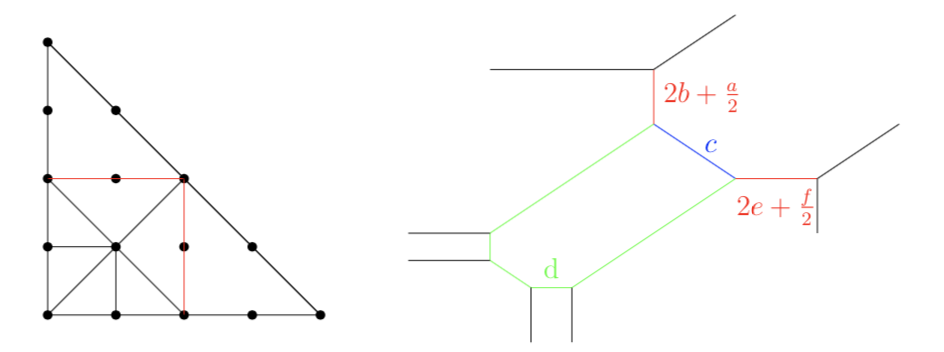
whose red edges reveal two lollis with wanted egdge and cycle lengths after modification \(x\mapsto x+1-t^b\) and \(y\mapsto y+1-t^e\).