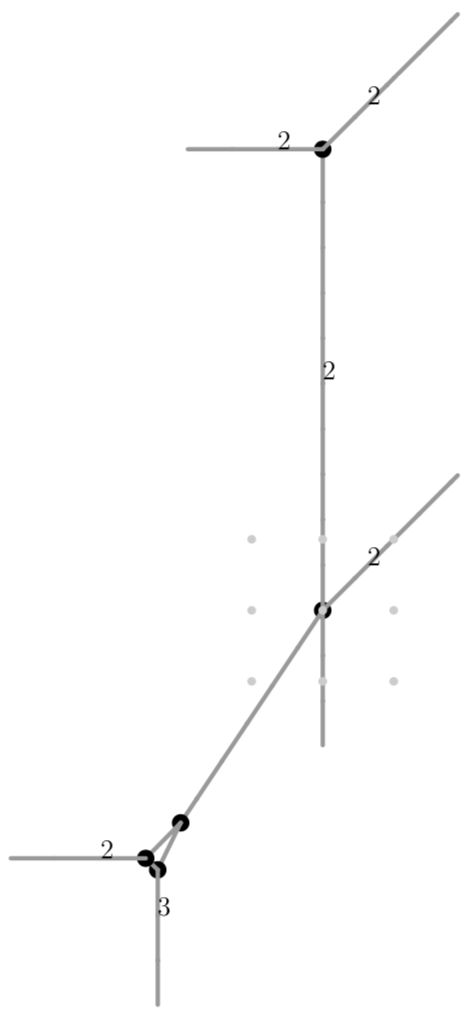
Type (303)

A tropical curve of type (303) is of the form

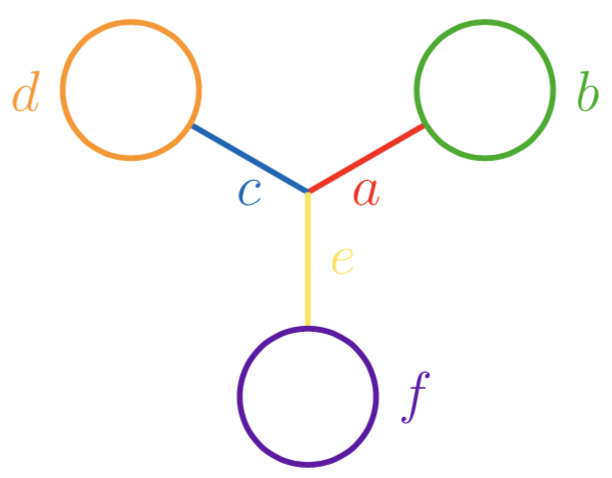
../_images/type303.png

Due to symmetry, we may assume \(a\geq c\geq e\). It is never embeddable as a tropical quartic curve in \(\mathbb{R}^2\).

To illustrate how a curve is embeddable in a tropical quartic curve as a tropical plane, consider the following configuration of lengths:

\[a=1, \quad b=1, \quad c=1, \quad d=2, \quad e=1, \quad f=3.\]

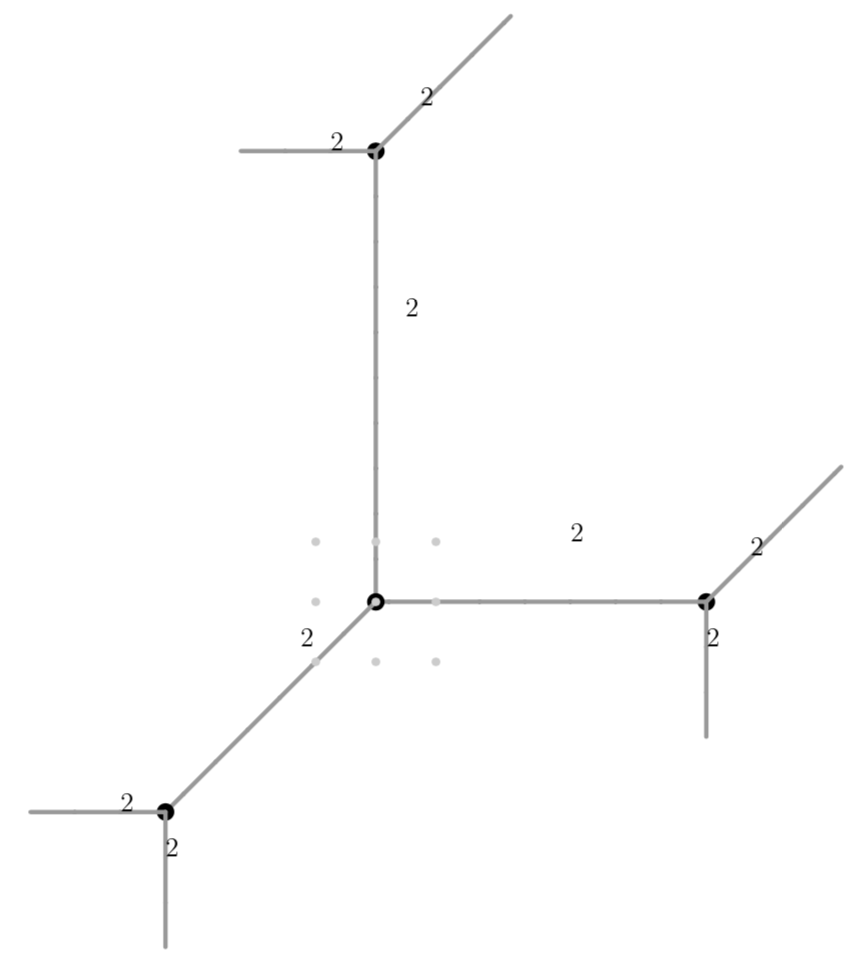
For that, consider the following quartic polynomial with its highly degenerate tropical quartic curve:

poly g = (t19)*x4+x2y2+(t13)*y4+(2t6+2t5+2t4+2t3+2t2+2t+2)*x2y+(2t4+2t3+2t2+2t+2)*xy2+(t12+2t11+3t10+4t9+5t8+6t7+6t6+6t5+5t4+4t3+3t2+2t+1)*x2+(-2t2-4t-2)*xy+(t8+2t7+3t6+4t5+4t4+4t3+3t2+2t+1)*y2+(t7);
drawTropicalCurve(g,"max");
\[\begin{split}g &= t^{19}x^4+x^2y^2+t^{13}y^4+(2t^6+2t^5+2t^4+2t^3+2t^2+2t+2)x^2y\\ &\quad +(2t^4+2t^3+2t^2+2t+2)xy^2\\ &\quad +(t^{12}+2t^{11}+3t^{10}+4t^9+5t^8+6t^7+6t^6+6t^5+5t^4+4t^3+3t^2+2t+1)x^2\\ &\quad +(-2t^2-4t-2)xy+(t^8+2t^7+3t^6+4t^5+4t^4+4t^3+3t^2+2t+1)y^2+t^7\end{split}\]
../_images/type303a.png

The modification \(z_1=x+1+t+t^3+t^4\), which goes along \(w_x=0\), yields the following tropical curve after projecting onto the \(z_1y\) plane (\(y\) remaining the vertical direction):

poly g1=substitute(g,x,x-1-t-t3-t4);
drawTropicalCurve(g1,"max");
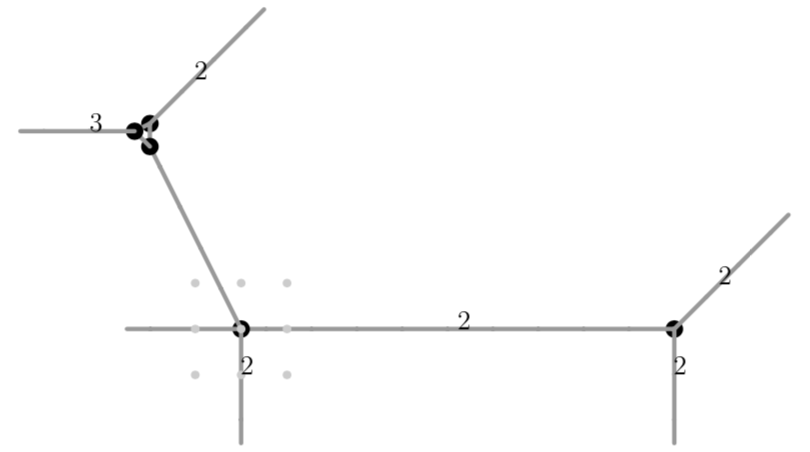
../_images/type303b.png

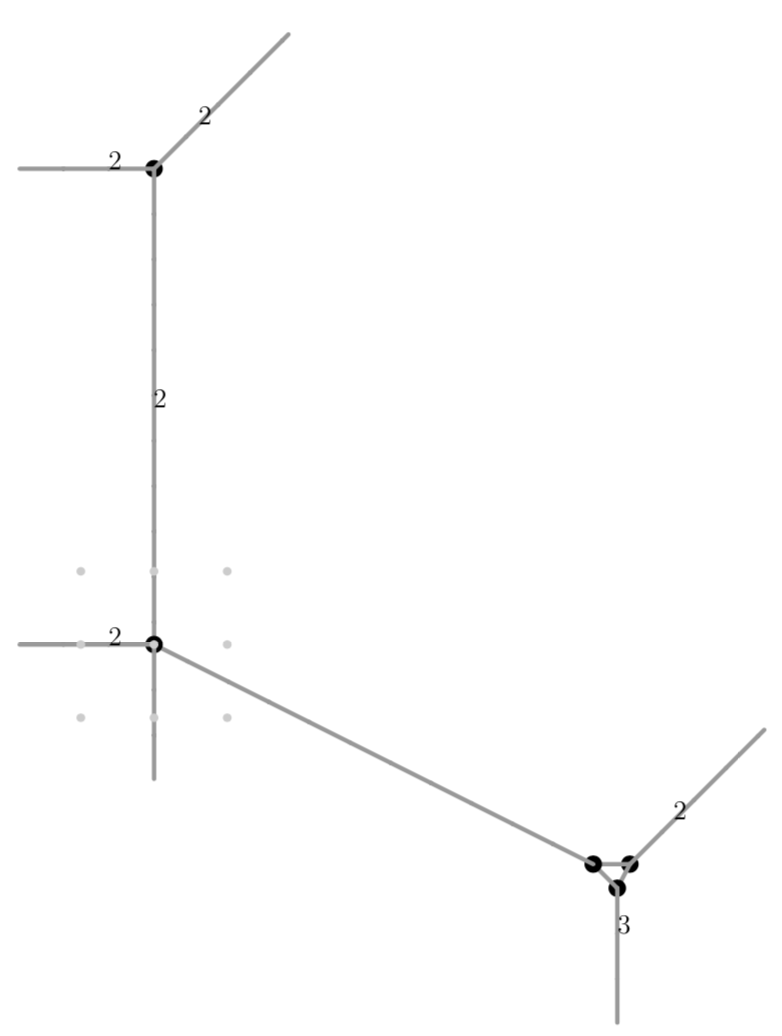
The entirety of \(w_x<0\) is mapped onto \(w_z=0\), while the edge on the line \(w_x=0\) with multiplicity \(2\) reveals a lolli with edge \(e\) of length \(1\) and cycle \(b\) of length \(1\).

Similarly, the modifications \(z_2=y+1+t++t^2+t^4+t^5+t^6\) and \(z_0=y-x-2itx\), where \(i\in\mathbb C\) denotes the imaginary number, will reveal lollis of desired edge and cycle lengths:

poly g2=substitute(g,y,y-1-t-t2-t4-t5-t6);
drawTropicalCurve(g2,"max");
../_images/type303c.png 
ring s = (0,i),(t,x,y),dp;
minpoly = i2+1;
poly g = imap(r,g);
poly g0 = substitute(g,y,y+x+2it*x);
g0 = subst(g0,i,15);
setring r;
poly g0 = imap(s,g0);
drawTropicalCurve(g0,"max");

(Note that we are cheating slightly in the final modification, as we are setting \(i=15\) when it comes to drawing the picture)

../_images/type303d.png