Solving two-parameter eigenvalue problems using an alternating method

This page contains auxiliary files to the paper:
Henrik Eisenmann and Yuji Nakatsukasa: Solving two-parameter eigenvalue problems using an alternating method
In: Linear algebra and its applications, 643 (2022), p. 137-160
MIS-Preprint: 83/2020 DOI: 10.1016/j.laa.2022.02.024 ARXIV: https://arxiv.org/abs/2008.03385 CODE: Notebook.

Contents:

We want to find solutions of the two-parameter eigenvalue problem

\[\begin{split}(A_1+\lambda B_1 + \mu C_1)u=0,\\ (A_2+\lambda B_2 + \mu C_2)v=0.\end{split}\]

The eigenvalues are the intersection points of the two eigencurves associated to each equation, here depicted in blue and orange:

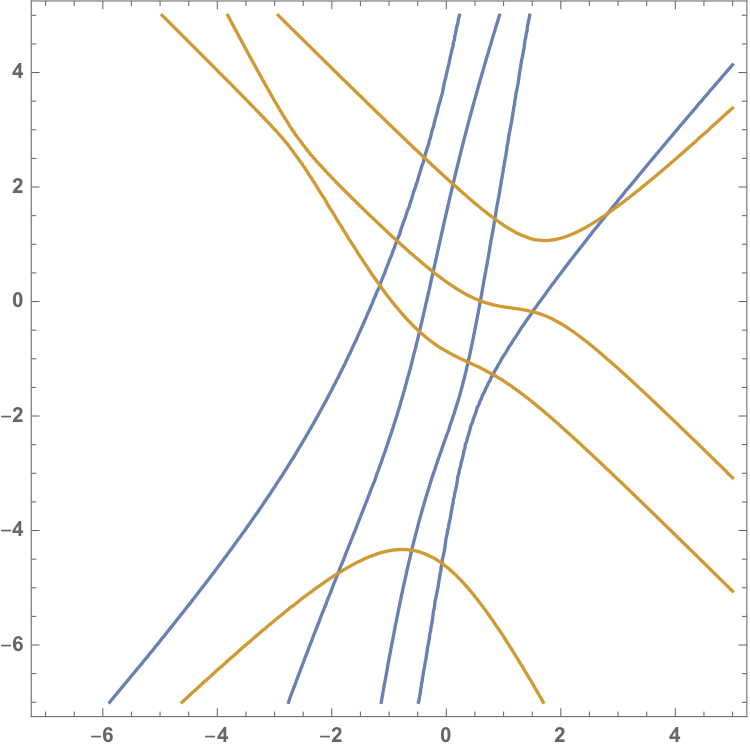
Alternative text

If the matrix \(C_1\otimes B_2-B_1\otimes C_2\) is definite, every yellow curve intersects every blue curve exactly once. The alternating algorithm can then be interpreted in the following way:

1: Start on a point on an orange curve.
2: Compute the intersection of the tangent to that point and a blue curve.
3: Compute the intersection of the tangent to that point and the orange curve.

And repeating. This is illustrated in the following picture:

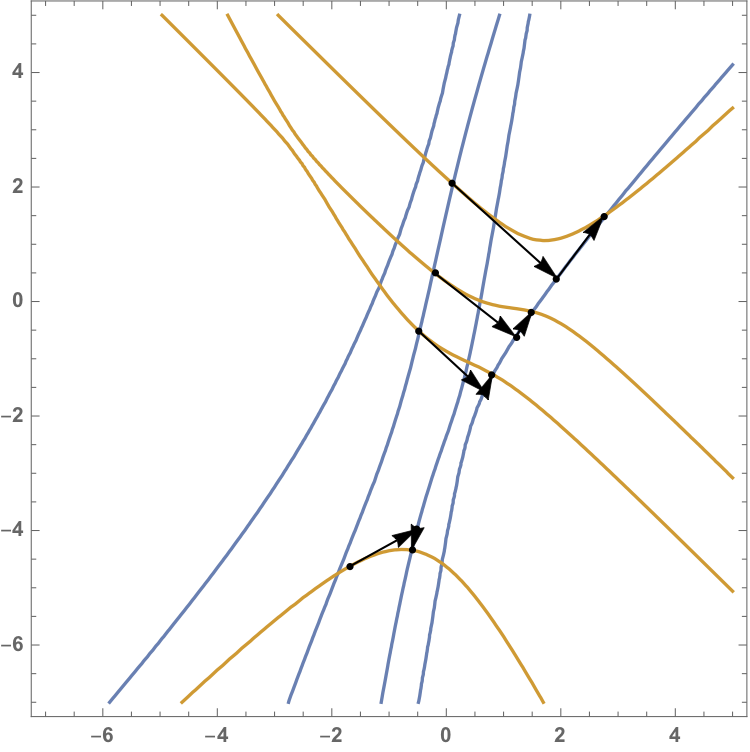
Alternative text

The arrows show the iterates. This interpretation allows us to provide a local quadratic convergence of our algorithm

The code is presented as a Jupyter notebook in Julia which can be downloaded here: TwoParameterNotebook.ipynb.

Project page created: 26/05/2021

Project contributors: Henrik Eisenmann, Yuji Nakatsukasa

Jupyter notebook written by: Henrik Eisenmann, 26/05/21

Software used: Julia (Version 1.5.2)

Corresponding author of this page: Henrik Eisenmann, henrik.eisenmann@mis.mpg.de