Cox Homotopies
We introduce Cox homotopies for solving sparse polynomial systems in a compact toric variety X. Our algorithms make explicit use of the Cox construction of X as a GIT quotient of a quasi-affine space by the action of a reductive group. A Cox homotopy tracks paths in the total coordinate space of X and can be seen as a homogeneous version of the standard polyhedral homotopy.
Only BKK-many paths are tracked, and all paths remain inside X. The figure below illustrates classical homotopy continuation in the projective plane. As we track a parameter \(\tau\) from 1 to 0, five solution curves approach infinity.
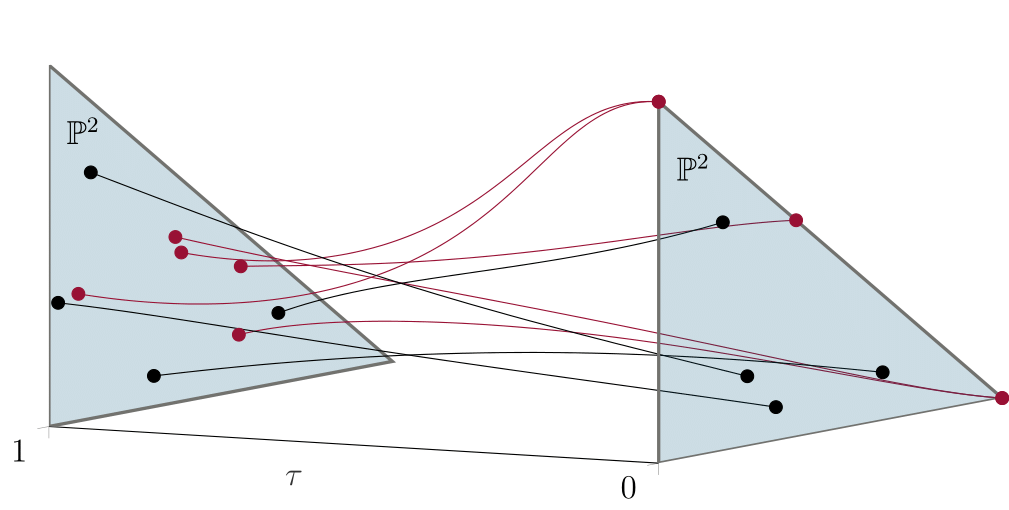
The following figure shows homotopy continuation in a compact toric variety, where only one solution curve approaches infinity—more precisely, some Cox coordinate of the endpoint is zero.
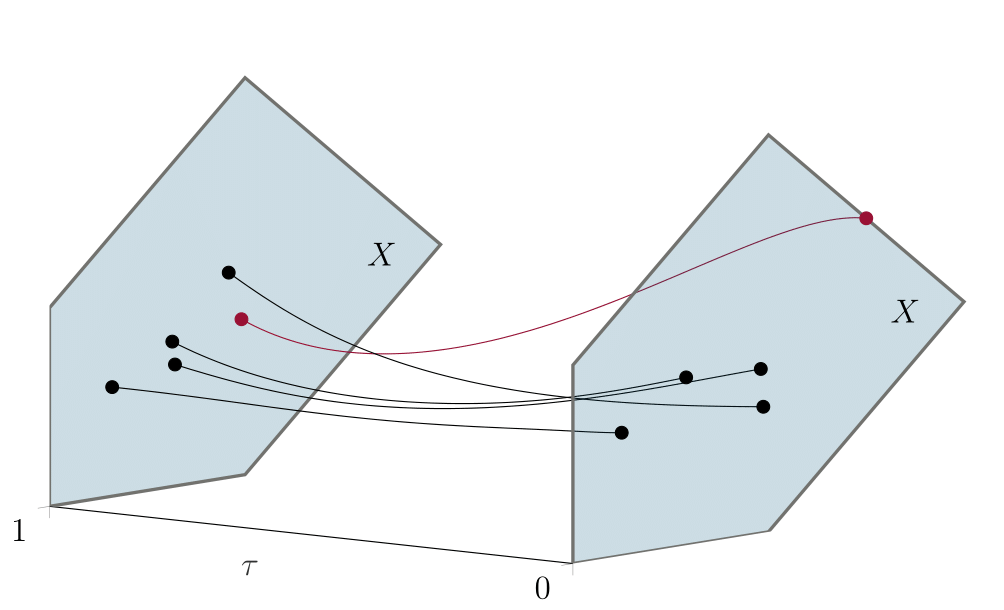
We implemented our Cox homotopy algorithm in julia using the packages HomotopyContinuation.jl and Polymake.jl. We include our implementation in this repository. Our algorithm has four advantages, each of which we highlight with example(s).
Avoid premature path truncation, see code for Experiments 1 and 3
Orthogonal slicing, see code for Experiment 2
Track only BKK-many paths, see code for Experiments 1-4
Heuristics for understanding solutions at infinity, see code for Experiment 4
The following Jupyter notebooks illustrate how our code, which may be downloaded here code.zip, can be used to reproduce Experiments 1-4.
Project page created: 08/12/2020
Project contributors: Tim Duff, Simon Telen, Elise Walker, and Thomas Yahl
Corresponding author of this page: Simon Telen, Simon.Telen@mis.mpg.de
Software used: Julia (Version 1.5.2)