The Gaussian entropy map in valued fields
Abstract: We exhibit the analog of the entropy map for multivariate Gaussian distributions on local fields. As in the real case, the image of this map lies in the supermodular cone and it determines the distribution of the push forward under the valuation map. In general, this map can be defined for non-archimedian valued fields whose valuation group is an additive subgroup of the real line, and it remains supermodular. We also explicitly compute the image of this map in dimension 3.
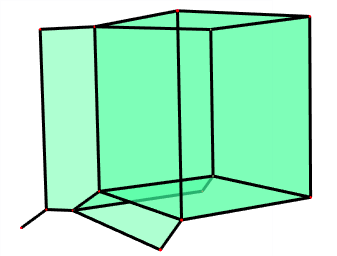
This repository includes our code to compute the entropy map (Section 3) when the field \(K\) is the field of Puiseux series in one variable with real coefficients. It also includes Polymake code to compute the image of the entropy map in dimension 3 (Section 5).
Our code is written in Julia (v1.6.2) (using the computer algebra system Oscar (v0.5.2)) and in Polymake (v4.3)
The following jupyter notebook contains code to compute entropy:
We also provide polymake code to visualize the image of the entropy map in \(d=3\) :
Project page created: 17/01/2022.
Project contributors: Yassine El Maazouz.
Corresponding author of this page: Yassine El Maazouz, yassine.el-maazouz@berkeley.edu
Software used: Julia (Version 1.6.2), Oscar (v0.5.2), Polymake(v4.3).