Toric Amplitudes and Universal Adjoints
This page contains auxiliary files to the paper:
Simon Telen: Toric Amplitudes and Universal Adjoints
ABSTRACT: A toric amplitude is a rational function associated to a simplicial polyhedral fan. The definition is inspired by scattering amplitudes in particle physics. We prove algebraic properties of such amplitudes and study the geometry of their zero loci. These hypersurfaces play the role of Warren’s adjoint via a dual volume interpretation. We investigate their Fano schemes and singular loci via the nef cone and toric irrelevant ideal of the fan.
Our Julia code relies on Oscar for computations with polyhedra, fans and polynomial ideals. It can be downloaded here: ToricAmplitudes.zip. The code can work with rational fans only. The file examples.jl illustrates how to use the code.
The toric amplitude of a simplicial fan \(\Sigma\) in \(\mathbb{R}^d\) is
\[\mathrm{Amp}_\Sigma \, = \, \sum_{\sigma \in \Sigma(d)} \frac{|\det U_\sigma|}{\prod_{\rho \in \sigma(1)} x_\rho}.\]
Here \(U \in \mathbb{R}^{n \times d}\) is a matrix whose rows generate the rays of \(\Sigma\). The universal adjoint is the polynomial \(\mathrm{Adj}_\Sigma = \Big ( \prod_{\rho \in \Sigma(1)} x_\rho \Big ) \cdot \mathrm{Amp}_\Sigma\).
The most important case is that in which \(\Sigma\) is the normal fan of a polytope \(P\). For instance, consider the three dimensional ABHY associahedron in the picture below:
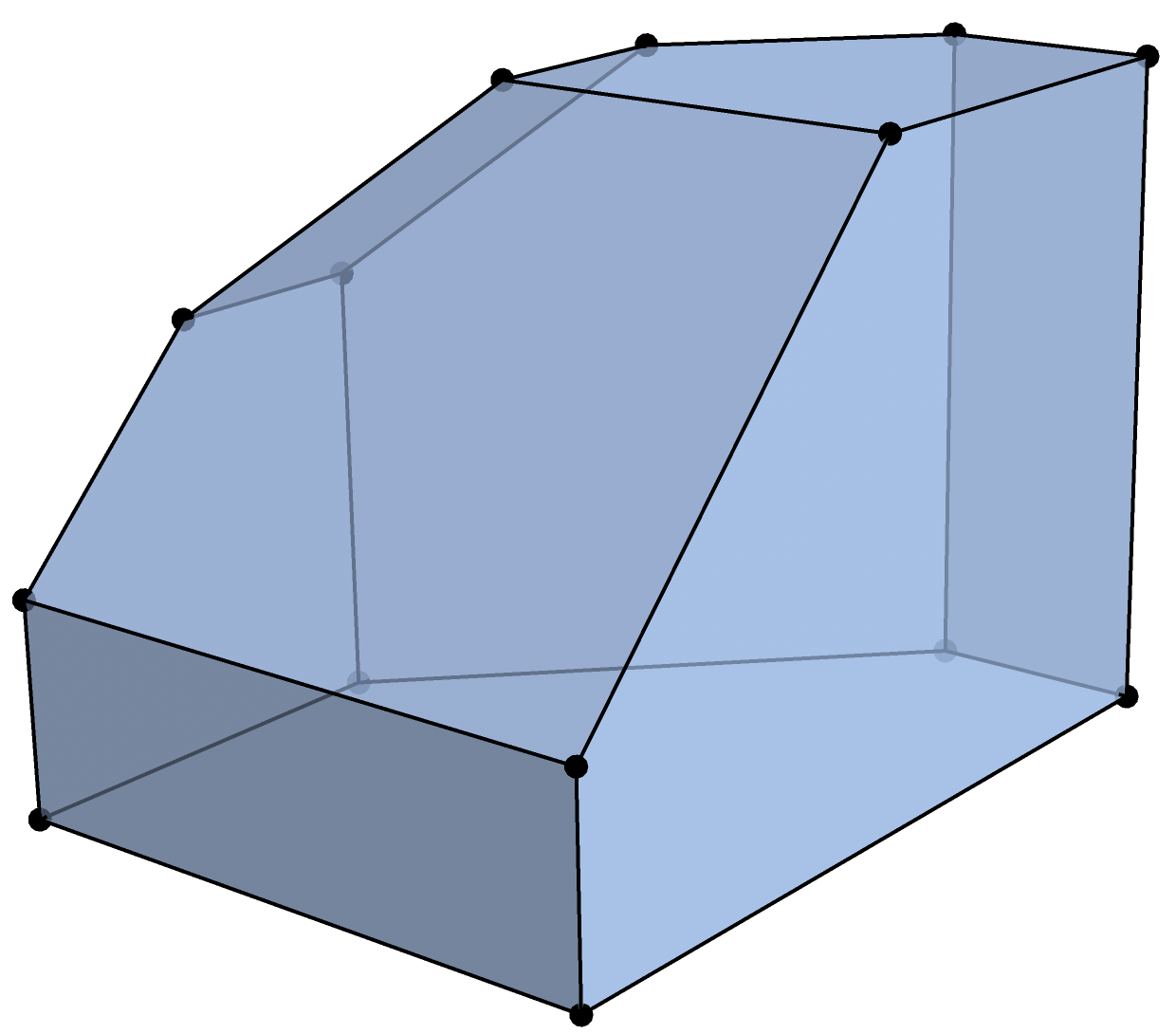
There are 9 facets, 21 edges and 14 vertices. This associahedron \(P\) has the following facet description:
\[\begin{split}\begin{pmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \\ 1 & -1 & 0 \\ 1 & 0 & -1 \\ 1 & 0 & 0 \\ 0 & 1 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} y_1 \\ y_2 \\ y_3 \end{pmatrix} + \begin{pmatrix} 3 \\ 4 \\ 3 \\ 2 \\ 2 \\ 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \geq 0.\end{split}\]
The \(9 \times 3\) matrix in this description is the ray generator matrix \(U\). The universal adjoint is a sextic in nine variables:
\[\begin{split}\begin{matrix} \mathrm{Adj}_P \, = \, x_{13} x_{14} x_{15} x_{24} x_{25} x_{35} + x_{13} x_{14} x_{15} x_{24} x_{25} x_{46} + x_{13} x_{14} x_{15} x_{24} x_{36} x_{46} + x_{13} x_{14} x_{15} x_{25} x_{35} x_{36} \\ + x_{13} x_{14} x_{15} x_{35} x_{36} x_{46} + x_{13} x_{14} x_{24} x_{26} x_{36} x_{46} + x_{13} x_{14} x_{26} x_{35} x_{36} x_{46} + x_{13} x_{15} x_{25} x_{26} x_{35} x_{36} + x_{13} x_{25} x_{26} x_{35} x_{36} x_{46} \\ + x_{14} x_{15} x_{24} x_{25} x_{26} x_{35} + x_{14} x_{15} x_{24} x_{25} x_{26} x_{46} + x_{14} x_{24} x_{25} x_{26} x_{36} x_{46} + x_{15} x_{24} x_{25} x_{26} x_{35} x_{36} + x_{24} x_{25} x_{26} x_{35} x_{36} x_{46}. \end{matrix}\end{split}\]
The singular locus of its hypersurface consists of 138 components. Their equations can be downloaded here.
Project page created: 01/04/2025.
Project contributors: Simon Telen.
Corresponding author of this page: Simon Telen, simon.telen@mis.mpg.de.
Software used: Julia (Version 1.11.0), Oscar (Version Oscar v1.3.1).
System setup used: MacBook Pro with macOS Monterey 12.6, Processor 2,8 GHz Intel Core i7, Memory 16 GB 2133 MHz LPDDR3, Graphics Intel HD Graphics 630 1536 MB.
Last updated 01/04/25.
