Tropical invariants for binary forms and reduction types of Picard curves

This page contains auxiliary files to the paper:

Paul Alexander Helminck, Yassine El Maazouz and Enis Kaya: Tropical invariants for binary quintics and reduction types of Picard curves

In: Glasgow mathematical journal, 66 (2024) 1, p. 65-87

DOI: 10.1017/S0017089523000344 ARXIV: https://arxiv.org/abs/2206.00420 CODE: https://mathrepo.mis.mpg.de/TropicalInvariantsPicardCurves/index.html

Abstract: In this paper, we express the reduction types of Picard curves in terms of tropical invariants associated to binary forms. These invariants are connected to Picard modular forms using recent work by Clery and van der Geer. We furthermore give a general framework for tropical invariants associated to group actions on arbitrary varieties. The previous problem fits in this general framework by mapping the space of binary forms to symmetrized versions of the Deligne–Mumford compactification \(\overline{M}_{0,n}\). We conjecture that the techniques introduced here can be used to find tropical invariants for binary forms of any degree.

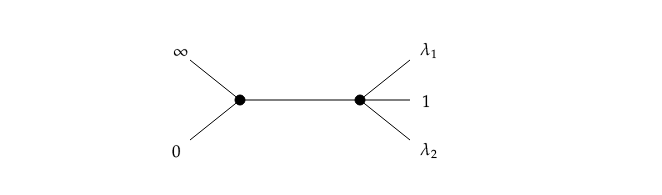
This repository includes our code to prove Theorems 1 and 2 by computing the invariants and universal families of binary quintics and Picard curves.

This repository includes our code to prove Theorems 1 and 2 by computing the invariants and universal families of binary quintics and Picard curves. Our code is written in Sage (version 9.4)

• Code for computations used in the proof of Theorems 1 and 3
• Code for computations used in the proof of Theorems 2 and 3
• Code to check the expressions of the invariants \(I_4,I_{8},I_{12},I_{18}\) in terms of \(j_2, j_3,j_5, j_6, j_9\)

• Computing the modular forms \(\nu(I_4), \nu(I_8), \nu(I_{12}), \nu(I_{18})\) and \(\nu(H)\).

Project page created: 23/05/2022.

Project contributors: Paul Alexander Helminck, Yassine El Maazouz and Enis Kaya.

Corresponding author of this page: Yassine El Maazouz, yassine.el-maazouz@berkeley.edu

Software used: SageMath (version 9.4).