Combinatorics of Correlated Equilibria
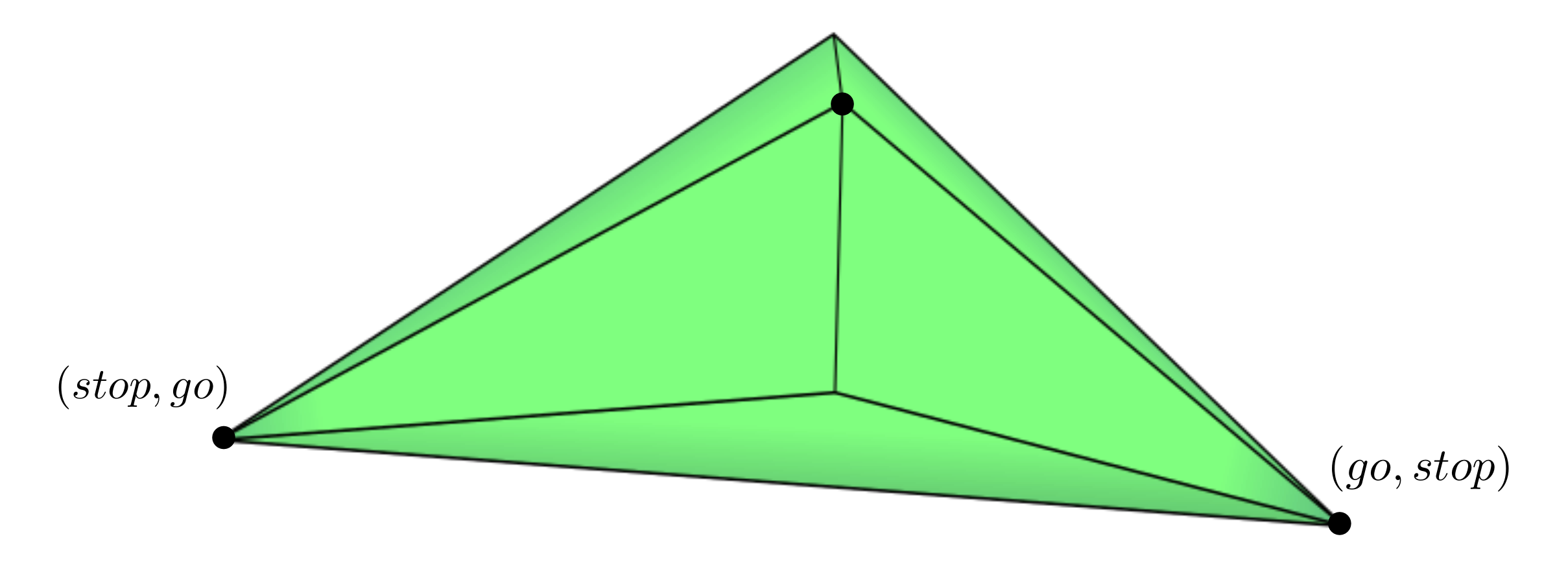
Abstract: We study the correlated equilibrium polytope \(P_G\) of a game \(G\) from a combinatorial viewpoint. We introduce the region of full-dimensionality for this class of polytopes, and prove that it is a semialgebraic set for any game. Through the use of the oriented matroid strata, we propose a structured method for describing combinatorial types of \(P_G\), and show that for \((2 \times n)\)-games, the algebraic boundary of each stratum is the union of coordinate hyperplanes and binomial hypersurfaces. We provide a computational proof that for \((2 \times 3)\)-games there exists a unique combinatorial type of maximal dimension.
Supplementary Material
This page contains supplementary material for the computations performed in the article. All files with ending .nb are run with \(\verb|Mathematica|\). Files endig with .py are run in \(\verb|SageMath|\) and diles endig with .m2 are run in \(\verb|Macaulay2|\). A file with ending .ipnynb is a Jupyter Notebook that is executed with a \(\verb|SageMath|\) kernel.
Computing the Polytope from Payoffs
We provide code to compute the correlated equilbrium polytope and the correlated equilibrium cone of a fixed \((d_1 \times \dots \times d_n)\)-game with payoff tensor in \(X\) in \(\verb|SageMath|\).
First, download the file correlated_polytope_cone.py and place it in the same folder as your Jupyter Notebook for SageMath. An example of a \((2 \times 3)\)-game can then be computed by the lines
from correlated_polytope_cone import *
D_i = [2,3]
X = [
[9,4], # X_{11} = [X_{11}^(1), X_{11}^(2)]
[4,0], # X_{12} = [X_{12}^(1), X_{12}^(2)]
[6,2], # X_{13} = [X_{13}^(1), X_{13}^(2)]
[5,5], # X_{21} = [X_{21}^(1), X_{21}^(2)]
[3,8], # X_{22} = [X_{22}^(1), X_{22}^(2)]
[9,7] # X_{23} = [X_{23}^(1), X_{23}^(2)]
]
P = correlated_equilibrium_polytope(D_i, X, base_ring = QQ)
C = correlated_equilibrium_cone(D_i, X, base_ring = QQ)
The input \(D\_i = [d_1,\dots,d_n]\) is the type of the game, e.g. D_i = [2,3] for a \((2 \times 3)\)-game as in the example above. X above corresponds to the payoff table.
Player 2 |
||||
\(s_1^{(2)}\) |
\(s_2^{(2)}\) |
\(s_3^{(2)}\) |
||
Player 1 |
\(s_1^{(1)}\) |
(9,4) |
(4,0) |
(6,2) |
\(s_2^{(1)}\) |
(5,5) |
(3,8) |
(9,7) |
|