Logarithmic Voronoi Cells
In this article, we study Voronoi cells in the statistical setting by considering preimages of the maximum likelihood estimator that tessellate an open probability simplex. In general, logarithmic Voronoi cells are convex sets. However, for certain algebraic models, namely finite models, models with ML degree 1, linear models, and log-linear (or toric) models, we show that logarithmic Voronoi cells are polytopes. As a corollary, the algebraic moment map has polytopes for both its fibres and its image, when restricted to the simplex. We also compute non-polytopal logarithmic Voronoi cells using numerical algebraic geometry. Finally, we determine logarithmic Voronoi polytopes for the finite model consisting of all empirical distributions of a fixed sample size. These polytopes are dual to the logarithmic root polytopes of Lie type A, and we characterize their faces.
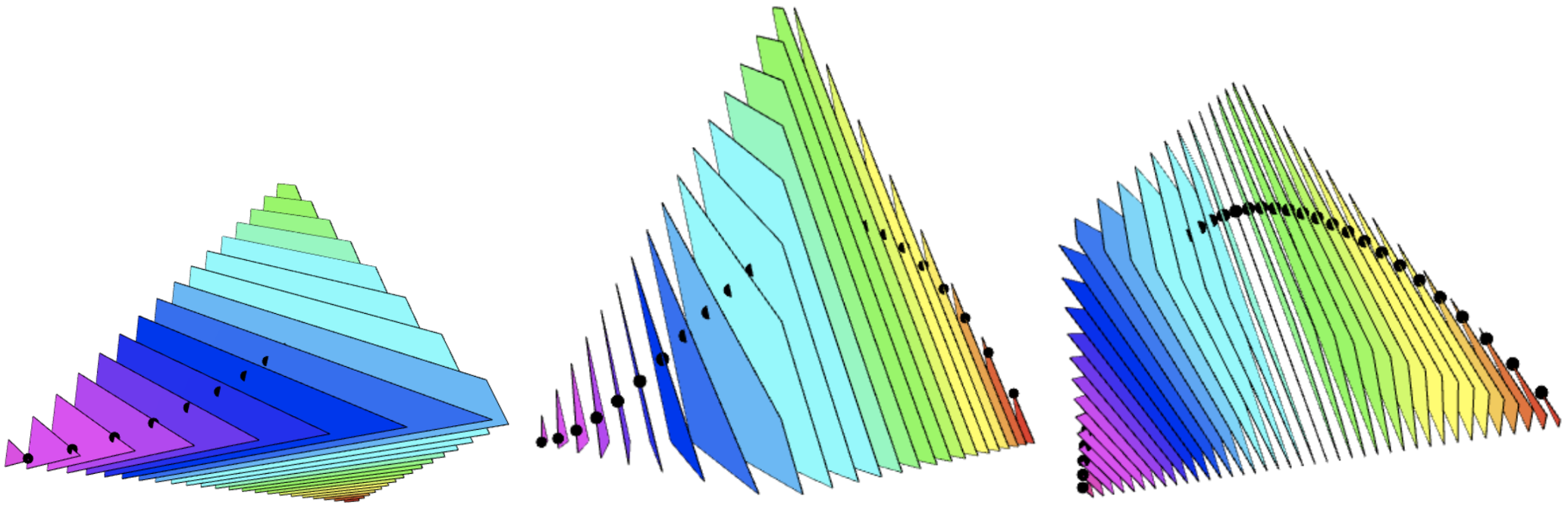
One major computation related to this paper is already available at the HomotopyContinuation.jl website, as a worked example: https://www.juliahomotopycontinuation.org/examples/logarithmic-voronoi/.
Here, we present another computation which aims to produce the following image of a nonlinear boundary for a logarithmic Voronoi cell. While our article focuses on cases when the logarithmic Voronoi cell is a polytope, there are many cases where it is not a polytope, this being one of them.
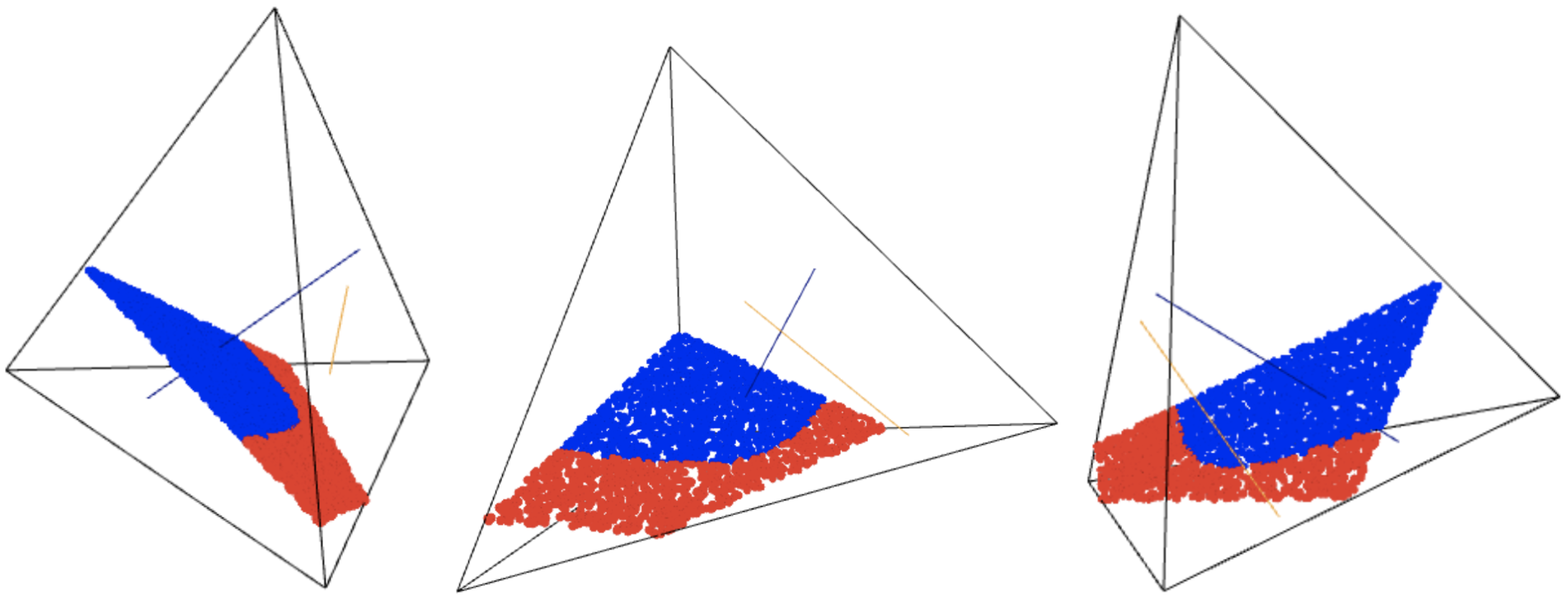
The Jupiter file making these computations can be seen by clicking the link below.
The Jupyter notebook can be downloaded here.
Alternatively, you can run the computations yourself by using the following link:
Project page created: 10/11/2020
Code contributors: Yulia Alexandr and Alexander Heaton
Jupyter Notebook written by: Alexander Heaton, 10/11/2020
Software used: SageMath 9.1.
Project contributors: Yulia Alexandr and Alexander Heaton
Corresponding author of this page: Alexander Heaton, alexheaton2@gmail.com