Tropical Quartics and Canonical Embeddings for Tropical Curves of Genus 3
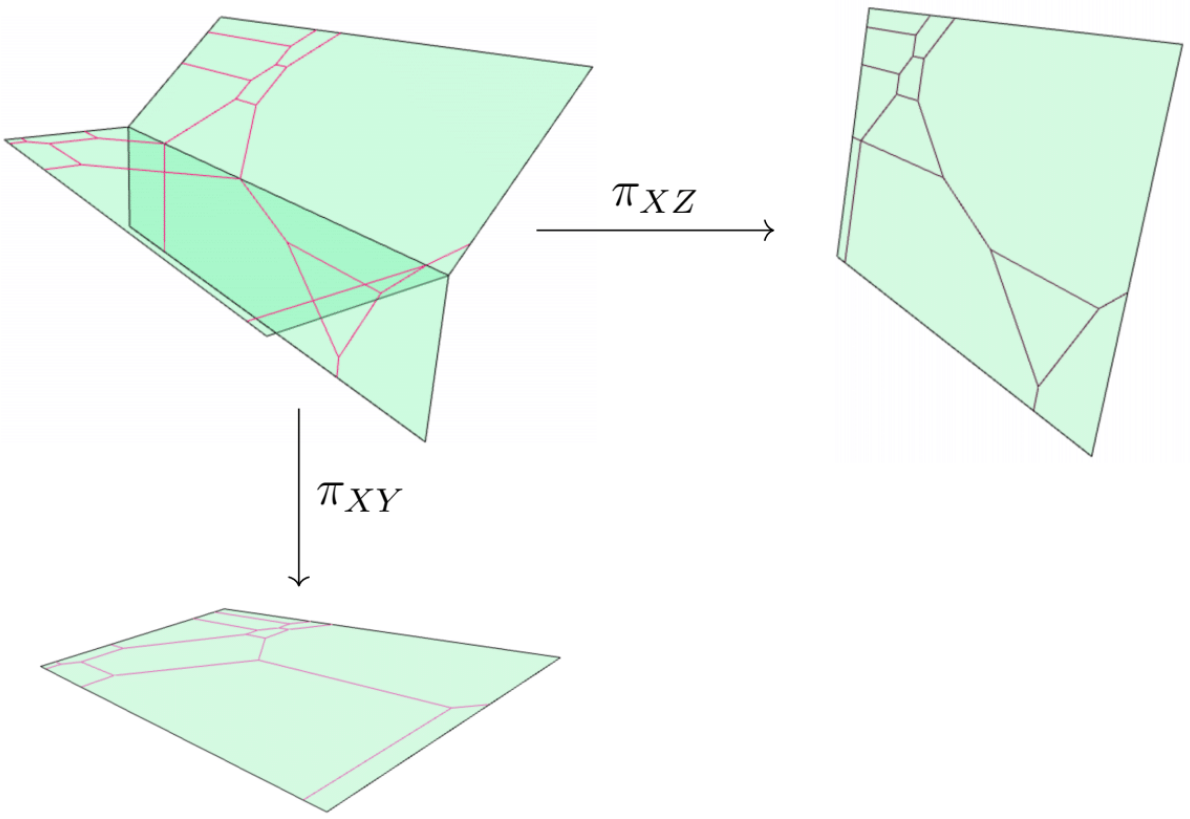
In [BJMS15] the authors study the moduli space of metric graphs that arise from tropical curves in \(\mathbb R^2\). In particular, they show that not all abstract tropical curves of genus 3 can be embedded as a tropical quartic in \(\mathbb R^2\) and offer a complete characterization of all curves which admit such an embedding.
we show that all tropical curves of genus 3, which are not “realizably hyperellipcitc”, can be embedded as tropical quartics in a tropical plane. This is done by explicit constructions for all curves which are not realizably hyperelliptic and obstructions for curves which are.
Here, we present examples for all our constructions, using the computer algebra system Singular and its library tropical.lib. All examples can be found bundled in the following Singular script.
We will exclusively work in the following ring and all code blocks on this website will require it to be the currently active base ring:
LIB "tropical.lib";
ring r = (0,t),(x,y),dp;
Project contributors: Marvin Anas Hahn, Hannah Markwig, Yue Ren, and Ilya Tyomkin
Software used: Singular